Можно показать, что формулы для моментов инерции
Іх =  cоs 2α +
cоs 2α + 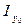 sin 2α,Іу =
sin 2α,Іу = 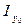 cоs 2α +
cоs 2α + 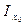 sin 2α., Іху =
sin 2α., Іху = 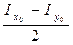 sin2α представляют уравнение окружности впараметрической форме. Поэтому вычисление моментов инерции по полученным аналитическим формулам можно заменить графическим определением этих величин в системе координат (Іх, Іу), Іху, построив круг, называемый кругом инерции.
sin2α представляют уравнение окружности впараметрической форме. Поэтому вычисление моментов инерции по полученным аналитическим формулам можно заменить графическим определением этих величин в системе координат (Іх, Іу), Іху, построив круг, называемый кругом инерции.
В графическом способе исследования моментов инерции рассматриваются прямая и обратная задачи.
Прямая задача: известны главные центральные моменты инерции  ,
, 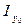 , требуется графическим способом найти моменты инерции Іх, Іу, Іху относительно осей х и у, повернутых от главных осей на угол α.
, требуется графическим способом найти моменты инерции Іх, Іу, Іху относительно осей х и у, повернутых от главных осей на угол α.
В координатной системе (Іх, Іу), Іху (рис.2.10) построим круг на диаметре АВ, отложив в масштабе отрезки ОА= 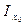 , ОВ =
, ОВ = 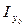 . В центре круга С от оси абсцисс отложим центральный угол 2α (α >0, если он откладывается против часовой стрелки), пересечение стороны этого угла с окружностью обозначим через Dх, а диаметрально ей расположенную точку через Dу. Проекции этих точек на ось абсцисс обозначим через Кх,, Ку.
. В центре круга С от оси абсцисс отложим центральный угол 2α (α >0, если он откладывается против часовой стрелки), пересечение стороны этого угла с окружностью обозначим через Dх, а диаметрально ей расположенную точку через Dу. Проекции этих точек на ось абсцисс обозначим через Кх,, Ку.
Докажем, что отрезки ОКх= Іх, ОКу= Іу, КхDх= Іху .
Из рис.2.10 видно, что ОКх=ОС + СКх, ОКу=ОС – СКу, ОС=ОВ+ВС,
|
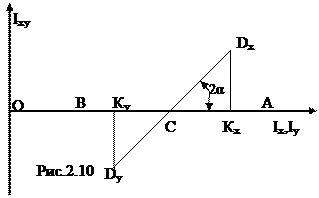 |
 |
Так как 1+cos2α =2 cos2α, 1-cos2α =2sin2α., то
ОКх = 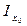 ∙ cos2α +
∙ cos2α + 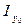 ∙sin2α = Іх,
∙sin2α = Іх,
ОКу =  ∙ sin2α +
∙ sin2α + 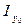 ∙cos2α = Іу,
∙cos2α = Іу,
DхКх = СDх ∙sin2α =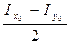 ∙sin2α = Іху
∙sin2α = Іху
Обратная задача: известны моменты инерции относительно центральных осей
Іх, Іу, Іху, необходимо определить главные центральные моменты инерции 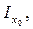
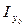 и положение главных центральных осей.
и положение главных центральных осей.
Отложим в масштабе по координатным осям (Іх, Іу), Іху отрезки ОКх= Іх, ОКу= Іу,
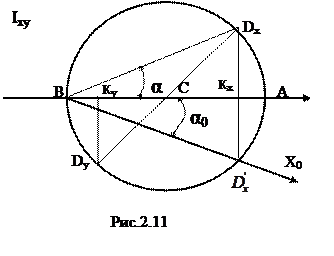
 КхDх = Іху, КуDу = - Іху (рис.2.11). На отрезке DХDУ как на диаметре построим круг и обозначим на оси абсцисс его крайние точки: крайнюю правую точкой А, крайнюю левую тоИз преды-дущей задачи следует: ОА=
КхDх = Іху, КуDу = - Іху (рис.2.11). На отрезке DХDУ как на диаметре построим круг и обозначим на оси абсцисс его крайние точки: крайнюю правую точкой А, крайнюю левую тоИз преды-дущей задачи следует: ОА= , ОВ=
, ОВ= 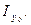 Найдем значения этих величин, выразив их через отрезки круга: ОА=ОС+СА,
Найдем значения этих величин, выразив их через отрезки круга: ОА=ОС+СА,
ОВ=ОС-ВС, СА=ВС=СDХ=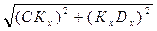 ,
,
СКх = СКу= 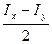 ,
,
тогда
СА=ВС=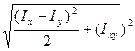 ,
,
ОС = ОКу + СКу = Іу +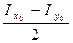 =
= 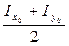 .
.
Используя значения полученных отрезков, запишем выражения для главных центральных моментов инерции
ОА=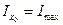
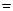 I
I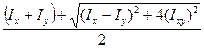 ,
,
ОВ= 
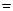 I
I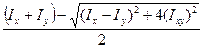 .
.
Из рис. 2.11 следует, что α0 = -α, тогда
tgα0 =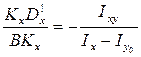 .
.
2.7 Радиусы и эллипс инерции
Осевые моменты инерции сечения можно представить как произведение площади сечения на квадрат некоторой величины, называемой радиусом инерции: Іх =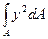 = =А
= =А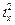 , где
, где 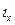 - радиус инерции относительно осих. Из этого выражения следует, что
- радиус инерции относительно осих. Из этого выражения следует, что 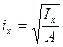 ,
, 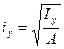 . Главным центральным осям будут соответствовать главные радиусы инерции
. Главным центральным осям будут соответствовать главные радиусы инерции
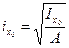 ,
, 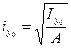 .
.
Выражение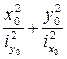 =1 представляет уравнение эллипса, полуосями которого являются главные радиусы инерции.
=1 представляет уравнение эллипса, полуосями которого являются главные радиусы инерции. 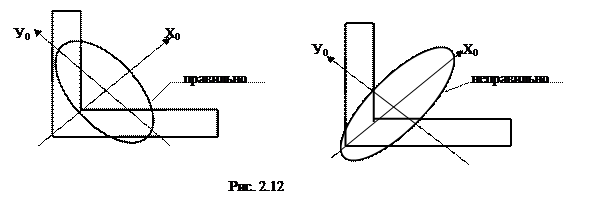
Эллипс, построенный на полуосях, равных главным радиусам инерции, называется эллипсом инерции.
Необходимо отметить, что при построении эллипса отрезки, равные 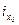 , откладываются по оси у0, а отрезки, равные
, откладываются по оси у0, а отрезки, равные 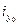 , - по оси х0. Поэтому эллипс инерции всегда вытянут вдоль сечения (рис.2.12), и он не может быть больше сечения, а так же заметно меньше его (рис.2.13).
, - по оси х0. Поэтому эллипс инерции всегда вытянут вдоль сечения (рис.2.12), и он не может быть больше сечения, а так же заметно меньше его (рис.2.13).
Для определения момента инерции относительно произвольной оси Х необходимо провести касательную α -α к эллипсу инерции, параллельную этой оси. Перпендикуляр СК, опущенный из центра эллипса С на эту касательную будет равен радиусу инерции, т.е., і х=СК, Iх=(СК)2А
 | |||
 | |||
|
|
|
|






 | |||||||||||||
| |||||||||||||
 |  | ||||||||||||
 |  | ||||||||||||
|
3.7 Моменты инерции сложных сечений
При проверке прочности элементов конструкций приходится встречаться с поперечными сечениямидовольно сложной формы, для которых нельзя вычислить моменты инерции таким простым путем, каким пользовались для треугольника, прямоугольника или круга. В этом случае сложное сечение разбивают на простые фигуры, для которых известны площади, координаты центров тяжестей и моменты инерции относительно собственных центральных осей 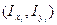 . По формулам (3.1) находят координаты центра тяжести c всего сечения в произвольно выбранных осях x0,y0, параллельных центральным осям
. По формулам (3.1) находят координаты центра тяжести c всего сечения в произвольно выбранных осях x0,y0, параллельных центральным осям 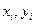 выделенных элементов. Через центр тяжести c проводят центральные оси сечения u, v, относительно которых вычисляют осевые и центробежный моменты инерции по формулам (3.15). Моменты инерции относительно главных центральных осей определяются по формулам (3.20), а положение главных центральных осей – по формуле (3.18).
выделенных элементов. Через центр тяжести c проводят центральные оси сечения u, v, относительно которых вычисляют осевые и центробежный моменты инерции по формулам (3.15). Моменты инерции относительно главных центральных осей определяются по формулам (3.20), а положение главных центральных осей – по формуле (3.18).
Пример. Для заданного сложного поперечного сечения, состоящего из двутавра №18 и уголка 100х100х12, вычислить значения главных центральных моментов инерции 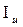 ,
,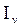 и положение главных центральных осей u, v.
и положение главных центральных осей u, v.
 2014-02-02
2014-02-02 5143
5143

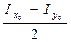 , тогда ОС=
, тогда ОС=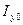 +
+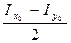 =
=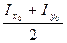 , CКх= СDхcos2α =
, CКх= СDхcos2α = 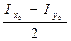 ∙cos2α, ОКх=
∙cos2α, ОКх=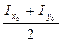 +
+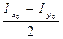 ∙cos2α = =
∙cos2α = = 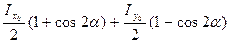 .
.