2014-02-02
592
Пусть заданы моменты инерции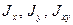 
. Требуется найти 
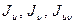, относительно осей, повернутых к заданным на угол 
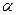(рис. 4.5).
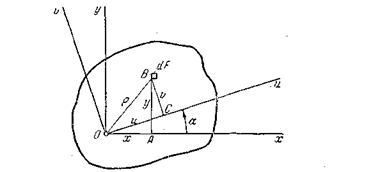
Рис. 4.5
Выберем произвольную площадку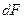 
и выразим ее координаты в новых осях 
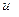и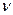 
через старые 
.
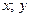Проектируем замкнутый четырехугольник 
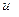на оси и 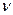. Так как проекция ломаной линии равна проекции замыкающей, находим:
.
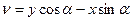
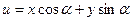В выражениях исключаем 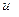и 
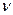
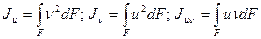тогда
,
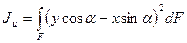
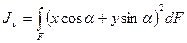
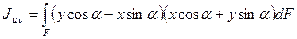откуда
(4.5)
Рассмотрим первые два уравнения из 4.5, складывая их почленно, получим:
.
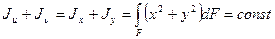Таким образом, при повороте осей сумма осевых моментов инерции относительно двух взаимно перпендикулярных осей остается постоянной. Заметим, что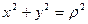 
, где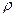 
— расстояние от элементарной площадки до точки 0.
Таким образом
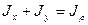, (4.6)
где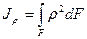 
— полярный момент инерции.
При помощи выражения 4.6 легко найти осевые моменты инерции для круга.
.
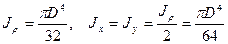С изменением 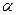каждая из величин 
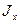и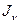 
меняется, а сумма их остается постоянной. Следовательно, существует такой угол 
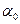, при котором один из элементов инерции достигает своего максимального значения, в то время как другой момент инерции принимает минимальное значение.
Дифференцируя первое выражение из 4.5 по 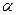, и приравнивая производную нулю, найдем
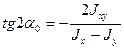(4.7)
При этом значение 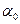один из осевых моментов достигает максимального значения, другой - минимального, а центробежный равен 0.
Оси, относительно которых центробежный момент инерции равен нулю, а осевые моменты принимают экстремальные значения, называются главными осями.
Найдем величины главных моментов инерции. Для этого первые две формулы из 4.5 приведем к виду
.
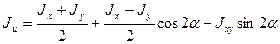
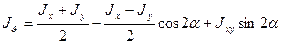Учитывая, что
,
.
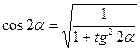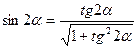Исключаем при помощи 4.7 угол 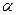, получим для определения значений главных моментов инерции.
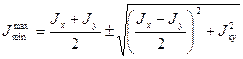. (4.8)
