Идеальным считается газ, который можно рассматривать как систему невзаимодействующих материальных точек, упруго сталкивающихся друг с другом и со стенками сосуда.
Уравнение состояния представляет собой функциональную зависимость, связывающую между собой термодинамические параметры: 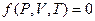 .
.
Экспериментально установлено, что для 1 моля идеального газа выполняется уравнение Клапейрона (уравнение состояния 1 моля идеального газа) 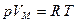 , (2.1.3)
, (2.1.3)
где 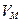 – молярный объем (объем 1 моля) газа;
– молярный объем (объем 1 моля) газа; 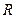 – универсальная газовая постоянная. Универсальность
– универсальная газовая постоянная. Универсальность 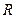 вытекает из закона Авогадро, согласно которому при одинаковых давлениях и температурах молярные объемы различных газов одинаковы. Подставив в это уравнение значения
вытекает из закона Авогадро, согласно которому при одинаковых давлениях и температурах молярные объемы различных газов одинаковы. Подставив в это уравнение значения 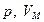 и
и 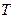 , соответствующие нормальным условиям, получим значение универсальной газовой постоянной
, соответствующие нормальным условиям, получим значение универсальной газовой постоянной 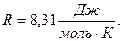
От уравнения состояния 1моля легко перейти к уравнению для любой массы 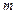 газа. При одинаковом давлении и температуре
газа. При одинаковом давлении и температуре 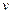 молей газа будут занимать в
молей газа будут занимать в 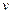 раз больший объем, чем один моль:
раз больший объем, чем один моль: 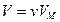 . Умножив обе части уравнения Клапейрона на
. Умножив обе части уравнения Клапейрона на 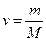
(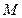 – молярная масса газа) и заменив
– молярная масса газа) и заменив 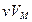 на
на  , получим уравнение состояния идеального газа (уравнение Менделеева – Клапейрона)
, получим уравнение состояния идеального газа (уравнение Менделеева – Клапейрона)  . (2.1.4)
. (2.1.4)
Разделим обе части уравнения Клапейрона на число Авогадро 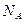 (число частиц, содержащихся в 1 моле)
(число частиц, содержащихся в 1 моле)  или
или  ,
,
где 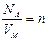 – концентрация молекул (число частиц газа, содержащихся в единичном объеме);
– концентрация молекул (число частиц газа, содержащихся в единичном объеме); 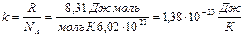 – постоянная Больцмана.
– постоянная Больцмана.
Следовательно, при постоянной температуре давление газа прямо пропорционально концентрации его молекул 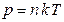 . (2.1.5)
. (2.1.5)
Это еще одна форма записи уравнения состояния идеального газа.
Выясним физический смысл универсальной газовой постоянной  .
.
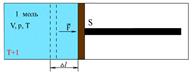 Рис.1.1 Рис.1.1 |
Пусть в цилиндре под поршнем находится 1 моль газа, с параметрами состояния 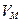 ,
, 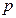 и
и 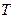 . При нагревании на
. При нагревании на 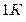 газ, изобарически расширяясь, сдвинет поршень на расстояние
газ, изобарически расширяясь, сдвинет поршень на расстояние 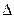
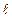 . Следовательно, сила
. Следовательно, сила 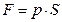 , действующая на поршень с площадью поперечного сечения
, действующая на поршень с площадью поперечного сечения 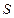 , совершит работу
, совершит работу 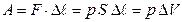 , (2.1.6)
, (2.1.6)
где 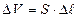 – изменение объема газа.
– изменение объема газа.
После нагревания газ займет объем 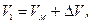 давление его не изменится. Запишем уравнения состояния 1 моля газа до нагревания и после него:
давление его не изменится. Запишем уравнения состояния 1 моля газа до нагревания и после него:
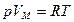 и
и  .
.
Вычтем из второго уравнения первое:  . (2.1.7)
. (2.1.7)
Выражения (2.1.5) и (2.1.7) совпали. Следовательно, универсальная газовая постоянная численно равна работе, которую совершает 1 моль идеального газа изобарически расширяясь при нагревании на 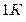 .
.
 2014-02-02
2014-02-02 968
968








