Уравнением волны называется выражение, описывающее зависимость смещения  колеблющейся частицы от координат
колеблющейся частицы от координат  и времени
и времени  :
:  . (1.9.2)
. (1.9.2)
Пусть точки, расположенные в плоскости 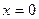 , совершают колебания по закону
, совершают колебания по закону  . Колебания частиц среды в точке
. Колебания частиц среды в точке 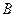 (рис.6.2), расположенной на расстоянии
(рис.6.2), расположенной на расстоянии  от источника колебаний
от источника колебаний  , будут происходить по тому же закону, но, будут отставать по времени от колебаний источника на
, будут происходить по тому же закону, но, будут отставать по времени от колебаний источника на 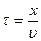 (где
(где 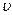 - скорость распространения волны). Уравнение колебания этих частиц имеет вид:
- скорость распространения волны). Уравнение колебания этих частиц имеет вид: 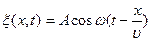 (1.9.3)
(1.9.3)
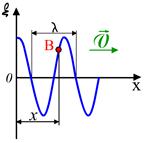 Рис.6.2
Рис.6.2
| Так как точка  была выбрана произвольно, то уравнение (1.9.3) позволяет определить смещение любой точки среды, вовлеченной в колебательный процесс, в любой момент времени, поэтому называется уравнением плоской бегущей волны. В общем случае оно имеет вид: была выбрана произвольно, то уравнение (1.9.3) позволяет определить смещение любой точки среды, вовлеченной в колебательный процесс, в любой момент времени, поэтому называется уравнением плоской бегущей волны. В общем случае оно имеет вид:  (1.9.4)
где (1.9.4)
где 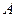 – амплитуда волны; – амплитуда волны;  – фаза плоской волны; – фаза плоской волны; 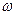 – циклическая частота волны; – циклическая частота волны;  – начальная фаза колебаний. – начальная фаза колебаний.
|
Подставляя в уравнение (1.9.4) выражения для скорости ( ) и циклической частоты (
) и циклической частоты ( ), получим:
), получим:  (1.9.5)
(1.9.5)
Если ввести волновое число 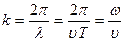 , то уравнение плоской волны можно записать в виде:
, то уравнение плоской волны можно записать в виде: 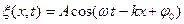 . (1.9.6)
. (1.9.6)
Скорость  в этих уравнениях представляет собой скорость перемещения фазы волны, и ее называют фазовой скоростью. Действительно, пусть в волновом процессе фаза постоянна
в этих уравнениях представляет собой скорость перемещения фазы волны, и ее называют фазовой скоростью. Действительно, пусть в волновом процессе фаза постоянна  . Для нахождения скорости ее перемещения разделим выражение для фазы на
. Для нахождения скорости ее перемещения разделим выражение для фазы на 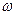 и продифференцируем по времени. Получим:
и продифференцируем по времени. Получим:
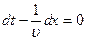 , откуда
, откуда 
 .
.
 2014-02-02
2014-02-02 620
620








