Если в среде одновременно распространяется несколько волн, то выполняется принцип суперпозиции (наложения): каждая волна ведет себя так, как будто другие волны отсутствуют, а результирующее смещение частиц среды в любой момент времени равно геометрической сумме смещений, которые получают частицы, участвуя в каждом из слагающих волновых процессов.
Большой практический интерес представляет наложение двух плоских волн
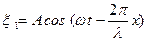 и
и 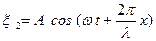 , (1.9.7)
, (1.9.7)
с одинаковыми частотами 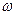 и амплитудами
и амплитудами 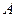 , распространяющихся навстречу друг другу вдоль оси
, распространяющихся навстречу друг другу вдоль оси  . Сложив эти уравнения, получим уравнение результирующей волны, называемой стоячей волной
. Сложив эти уравнения, получим уравнение результирующей волны, называемой стоячей волной 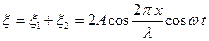 . (1.9.8)
. (1.9.8)
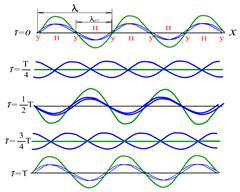 Рис.6.3 Рис.6.3 | Амплитуда стоячей волны 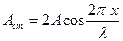 (1.9.9) является периодической функцией координаты (1.9.9) является периодической функцией координаты  и не зависит от времени. В точках среды, где и не зависит от времени. В точках среды, где 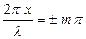  , амплитуда волны достигает максимального значения ( , амплитуда волны достигает максимального значения ( ). Эти точки называются пучностями ( ). Эти точки называются пучностями ( ) стоячей волны. Координаты пучностей ) стоячей волны. Координаты пучностей 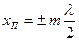 . . |
Таблица 5.1
В бегущей волне 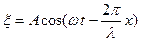 | В стоячей волне 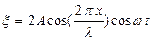 |
| Амплитуда колебаний | |
Все точки среды колеблются с одинаковыми амплитудами 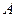 | Все точки среды колеблются с разными амплитудами 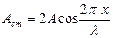 |
| Фаза колебаний | |
Фаза колебаний  зависит от координаты зависит от координаты  рассматриваемой точки рассматриваемой точки | Все точки между двумя узлами колеблются в одинаковой фазе 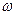 . При переходе через узел фаза колебаний изменяется на . При переходе через узел фаза колебаний изменяется на 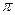 . . |
| Перенос энергии | |
| Энергия колебательного движения переносится в направлении распространения волны. | Переноса энергии нет, лишь в пределах 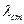 происходят взаимные превращения энергии. происходят взаимные превращения энергии. |
В точках среды, где 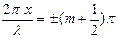
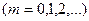 амплитуда волны обращается в ноль (
амплитуда волны обращается в ноль (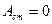 ). Эти точки называются узлами (
). Эти точки называются узлами (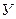 ) стоячей волны. Координаты узлов
) стоячей волны. Координаты узлов 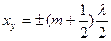 .
.
Расстояние между двумя соседними узлами (или между двумя соседними пучностями), называемое длиной стоячей волны, равно половине длины 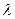 бегущей волны
бегущей волны  . Таким образом, при сложении двух бегущих волн образуется стоячая волна, узлы и пучности которой находятся все время в одних и тех же местах.
. Таким образом, при сложении двух бегущих волн образуется стоячая волна, узлы и пучности которой находятся все время в одних и тех же местах.
Характеристики бегущей и стоячей волн приведены в табл.5.1.
Часть II. Молекулярная физика и термодинамика
В молекулярной физике изучаются строение и свойства вещества, исходя из молекулярно-кинетических представлений, согласно которым все тела состоят из огромного числа непрерывно и хаотически движущихся частиц. Законы их поведения изучаются с помощью статистического метода.
В термодинамике изучаются общие свойства равновесных макроскопических систем и процессы перехода между различными термодинамическими состояниями. Термодинамика базируется на двух началах – фундаментальных законах, установленных в результате обобщения опытных данных. Молекулярно-кинетическая теория и термодинамика взаимно дополняют друг друга, образуя единое целое.
I. Термодинамические системы и их параметры
Мысленно выделенная макроскопическая система, рассматриваемая методами термодинамики, называется термодинамической системой. Обмен энергией и веществом может происходить как между частями внутри самой системы, так и между системой и внешней средой.
 2014-02-02
2014-02-02 2179
2179
