2014-02-02
508
Пусть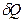 
– элементарное количество теплоты, сообщаемое нагревателем системе при малом изменении ее состояния, а 
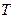– температура нагревателя. Если процесс обратим, то температура системы тоже равна 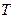. Обозначим элементарное приведенное количество теплоты 
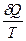в обратимом процессе через 
: 
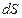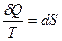, (2.4.4)
где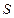 
– энтропия.
Покажем, что изменение энтропии 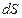является полным дифференциалом. Действительно, для 1 моля идеального газа
.
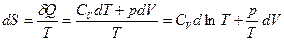Подставим в эту формулу выражение для (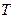
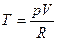), полученное из уравнения состояния 
.
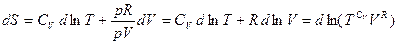Из этого выражения видно, что 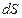– полный дифференциал. Таким образом, температура 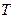является интегрирующим делителем, который обращает элементарную теплоту 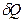в полный дифференциал 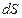. Следовательно, энтропия 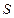является функцией состояния системы, в отличие от теплоты 
, являющейся функцией процесса. Энтропия имеет фундаментальное значение в физике.
