Циркуляцией вектора 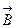 , по заданному замкнутому контуру называется интеграл
, по заданному замкнутому контуру называется интеграл
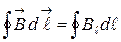 , (4.6.1)
, (4.6.1)
где  = Вcosa - составляющая вектора
= Вcosa - составляющая вектора 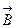 в направлении касательной к контуру,
в направлении касательной к контуру, 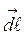 - вектор элементарной длины контура (в направлении обхода контура), a - угол между векторами
- вектор элементарной длины контура (в направлении обхода контура), a - угол между векторами 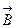 и
и  .Наиболее просто вычислить этот интеграл для магнитного поля, прямого проводника с током. Пусть прямой проводник перпендикулярен плоскости чертежа, ток направлен к нам (рис.20.14). Замкнутый контур представим в виде окружности радиуса r.
.Наиболее просто вычислить этот интеграл для магнитного поля, прямого проводника с током. Пусть прямой проводник перпендикулярен плоскости чертежа, ток направлен к нам (рис.20.14). Замкнутый контур представим в виде окружности радиуса r.
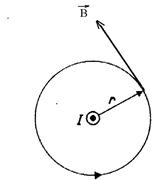 |
Рис.20.14
Вектор 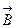 в каждой точке этого контура одинаков по модулю и направлен по касательной к окружности (
в каждой точке этого контура одинаков по модулю и направлен по касательной к окружности (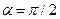 ). Циркуляция вектора
). Циркуляция вектора 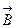 равна:
равна:
 . (4.6.2)
. (4.6.2)
Если контур тока не охватывает, то циркуляция вектора 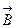 равна нулю. Можно показать, что формула (4.6.2) справедлива и для тока, текущего по проводнику произвольной формы. Сформулируем закон полного тока для магнитного поля в вакууме: циркуляция вектора
равна нулю. Можно показать, что формула (4.6.2) справедлива и для тока, текущего по проводнику произвольной формы. Сформулируем закон полного тока для магнитного поля в вакууме: циркуляция вектора 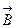 по произвольному замкнутому контуру равна произведению магнитной постоянной m0 на алгебраическую сумму токов, охватываемых этим контуром.
по произвольному замкнутому контуру равна произведению магнитной постоянной m0 на алгебраическую сумму токов, охватываемых этим контуром.
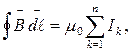 (4.6.3)
(4.6.3)
где n – общее число проводников с током, охватываемых контуром произвольной формы. Если ток охватывает контур несколько раз, то он должен учитываться столько же раз. Необходимо соблюдать правило знаков: положительным считается ток, направление которого связано с направлением обхода контура известным правилом правого винт
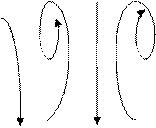 I1 I2 I3 I4
I1 I2 I3 I4
 |
Рис.20.15
На рис (20.15) изображен контур, охватывающий несколько токов. Направление обхода - против часовой стрелки. Алгебраическая сумма токов:
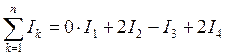 .
.
 2014-02-02
2014-02-02 709
709








