Парадокс Брайеса

Пример.

Поездка в часы «пик», когда, например, на автомагистрали имеют место автомобильные пробки.

В 1968 году американский специалист по транспортной логистике Брайес опубликовал парадокс, возникающий при планировании перевозок.

Парадокс заключается в том, что добавление дуги к сети может повлечь за собой увеличение общих расходов для каждого пользователя.

Приведем пример парадокса Брайеса (Рисунок 23).

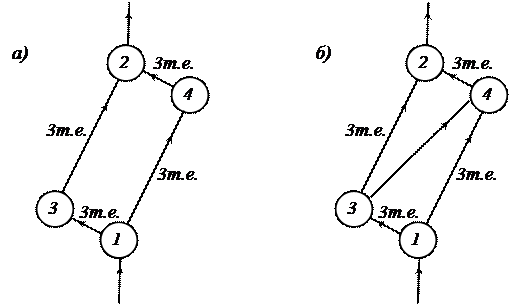
Рисунок 23. Парадокс Брайеса:

а) исходная сеть;

б) сеть с добавленной дугой 34

Заданы следующие соотношения по расходам пользователей:

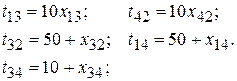
Задан поток величиной в 6 единиц из пункта 1 в пункт 2. В случае а) дуга 34 отсутствует.

Рассмотрим решение по дескриптивному распределению. Оно будет состоять в том, что поток по дугам 132 и 142 будут одинаковыми, т.е. по 3 единицы транспортных средств.

При этом расходы пользователей составят:

по дуге 132 –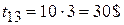

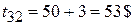
Итого 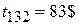на каждую единицу транспортных средств:

по дуге 142 –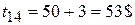

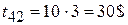
Итого 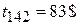на каждую единицу транспортных средств.

Общие расходы пользователей сети составят:

.

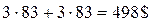Теперь рассмотрим случай, когда в сеть добавляется дуга 34.

Точно так же рассмотрим решение по дескриптивному распределению потоков в сети (Рисунок 24).

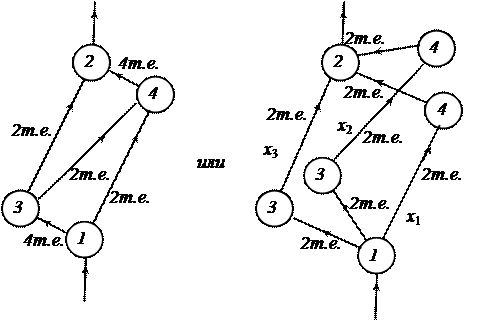
Рисунок 24. Парадокс Брайеса, случай б)

Определим расходы пользователей:

по дуге 132 –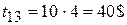

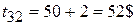
Итого ;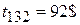

по дуге 142 –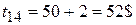

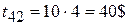
Итого ;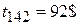

по дуге 1342 –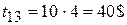

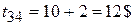
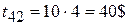
Итого .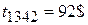

Общие расходы пользователей составят:

.

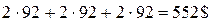Таким образом, добавление в сеть дуги 34 увеличивает общие расходы пользователей на 11% (552>498).

Запишем теперь для второго случая (при наличии дуги 34) задачу нормативного распределения и задачу дескриптивного распределения как оптимизационные задачи. Для удобства введем следующие обозначения (Рисунок 21): поток по дуге 142 – 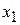; поток по дуге 1342 – 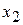; поток по дуге 132 – .

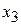В рассматриваемом случае единственное ограничение на непрерывность потоков дает:

.

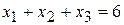Кроме того, есть ограничение на неотрицательность потоков, то есть:

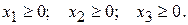
Тогда задача нормативного распределения потоков в сети принимает вид:

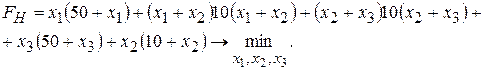
Это последнее выражение после раскрытия скобок принимает вид:

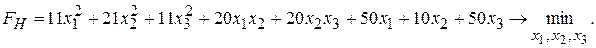
Отсюда видно, что целевая функция становится нелинейной, а записанные выше ограничения задачи являются линейными. Таким образом, в данном случае имеет место задача нелинейного программирования.

В случае дескриптивного распределения потоков на сети в рассматриваемом случае, получим следующее выражение для целевой функции задачи:

.

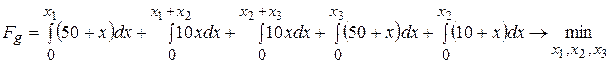Ограничения в данном случае остаются прежними.

Вычислим записанные выше интегралы и в результате получим:

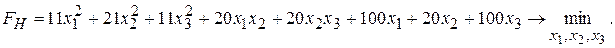
Из анализа записанных выше целевых функци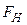й и 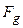видно, что это две различные задачи. И их решения не всегда могут совпадать.

Для 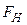решение будет следующим:

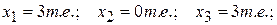
для 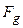решение будет следующим:

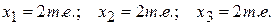
Отсюда видно, что при нормативном распределении потоков в сети (так называемая общественная оптимизация) поток на дуге 34 отсутствует. И наоборот, при дескриптивном распределении по дуге 34 имеет место поток в 2т.е.