Метод ветвей и границ

«Ветви и границы» – это метод, в котором все возможные решения комбинаторной оптимизационной задачи проверяется весьма разумным способом. Чтобы объяснить метод «ветвей и границ», рассмотрим задачу минимизации суммарных расходов пользователей сети. То есть будем минимизировать функцию 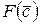путем выбора вектора , который принадлежит множеству 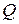всех возможных допустимых решений:

.

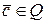Напомним, что в данном случае вектор – это вектор уровней технической оснащенности дуг сети , .

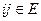Для начала поделим множество 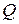на n подмножеств 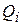, где

.

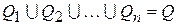Такой процесс называется «ветвлением».

Далее для каждого подмножества 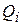вычислим нижнюю границу целевой функции (суммарной издержки) 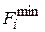, такую, что

, .

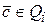Затем вычисляем верхнюю границу sup F для оптимального решения.

При этом sup F является значением целевой функции суммарных издержек в точке допустимого решения.

Далее начинается процесс отбора подмножеств путем сравнения sup F и 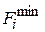для каждого подмножества :

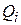Ø если , то подмножество 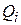не может содержать оптимальное значение искомого вектора ;

Ø если , то подмножество 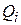может содержать вектор .

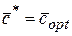Те подмножества 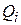, которые не могут содержать оптимальное решение, больше в проверке не нуждается. Они называются неактивными.

Другие, оставшиеся подмножества, называются активными и их исследуют дальше.

Если нас не интересуют все возможные оптимальные решения (с одними и теми же значениями целевой функции), а интересует только глобальный экстремум, то можно отбросить подмножества, для которых 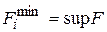, оставляя только те, для которых сохраняется строгое равенство

.

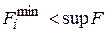Далее берется одно из активных подмножеств 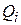и делится на ряд подмножеств :

, .

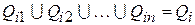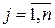Снова вычисляется нижняя грань целевой функции в каждом из n подмножеств, и затем выполняется процесс отбора, описанный ранее.

Вычисление прекращается, когда оптимальное решение найдено, и

для всех i.

В этом случае

,

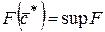где sup F – верхняя граница для оптимального решения.

Эффективность метода «ветвей и границ» очень сильно зависит от способа вычисления нижних и верхних границ:

, .

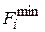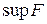Другой важный фактор, который влияет на эффективность – это метод ветвления.

Проиллюстрируем процедуру ветвей и границ графически (Рисунок 27).

Существует другое очень полезное свойство метода «ветвей и границ». Допустим, что удовлетворительным может быть решение, отличное от оптимального на 10%. Тогда можно будет заметить первоначальную верхнюю границу sup F на 0,9sup F и таким образом отбросить больше подмножеств 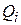. Эта процедура существенно сокращает время счета.

Метод «ветвей и границ» относится к методам дискретного программирования, к так называемой группе методов частичного перебора.

Геометрическая интерпретация метода «ветвей и границ» может быть следующей (Рисунок 28).

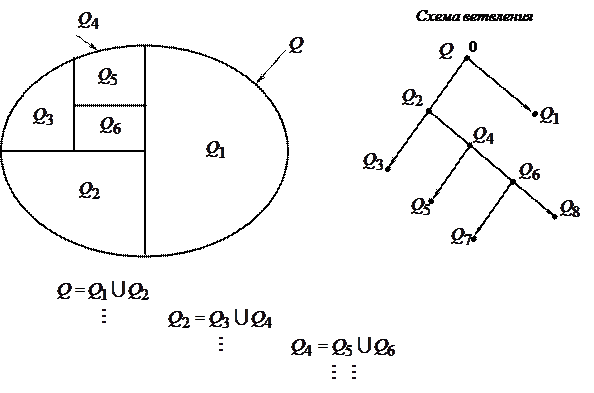
Рисунок 27. Схема «ветвления» исходного множества

Рисунок 28. Иллюстрация метода «ветвей и границ»

Для первого интервала 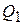имеем

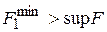
следовательно, этот интервал является неактивным. Для второго интервала 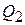– аналогично

.

Для ситуация обратная, т.е.

.

Отметим для дальнейшего, что sup F – это может быть наибольшая из возможных (на данном интервале) цена перевозки из А в В.

Из предыдущего неравенства следует, что рассматриваемый интервал является активным, и его следует подвергнуть процедуре разбиения на подинтервалы.

Что в этом случае представляет множество 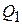? Или вообще? Это множества, соответствующие определенной, лучше сказать, заданной технической оснащенности дорог (все это для нашего примера).

Открытым в этом методе остается вопрос о нахождении sup F.