Построение множества действительных чисел

Лекции 8-9.

Поскольку ≈ - есть отношение эквивалентности на множестве 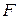, имеют место классы эквивалентности:

.

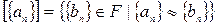Определение. Действительными числами назовем элементы фактормножества .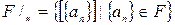

Определим на множестве действительных чисел действия сложения и умножения по следующим правилам:

,

.

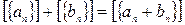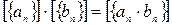Теорема 1. Сложение и умножение являются бинарными операциями на множестве .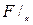

Доказательство.

Сложение и умножение определены, т.к. определены сложение и умножение любых рациональных чисел.

Согласно теореме 8, приведенной в лекциях 7, а также условию 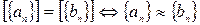, однозначность доказана.

Поскольку 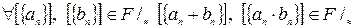в силу того, что сумма и произведение рациональных чисел также являются рациональными числами, множество 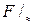замкнуто относительно сложения и умножения.

что и требовалось доказать.