2014-02-02
483
Теорема 8. Любая фундаментальная последовательность действительных чисел сходится в поле действительных чисел.
Доказательство.
Пусть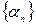 
- ф.п. д. ч., где 
:
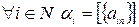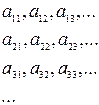
Рассмотрим последовательность 
. Покажем, что она фундаментальна.
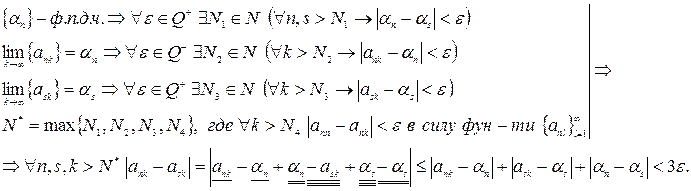Последнее неравенство влечет фундаментальность последовательностей вида 
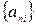при фиксированном 
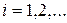. Оценим теперь 
:
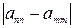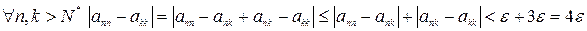. Таким образом, последовательность фундаментальна. Докажем, что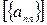 
и есть предел последовательности 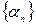. Пусть 
.
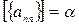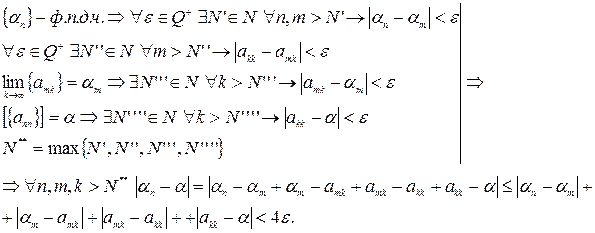
Последнее неравенство доказывает, что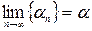 
.
что и требовалось доказать.
