2014-02-02
905
Лекция 10.
Возможны различные подходы к определению поля комплексных чисел.
Один из возможных заключается в следующем:
Определение. Полем комплексных чисел называется алгебраическое расширение поля действительных чисел, иначе, поле комплексных чисел наименьшее из полей, содержащее все алгебраические элементы над полем действительных чисел (т.е. все корни многочленов с действительными коэффициентами).
В этом случа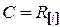е 
, где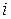 
- корень многочлена 
.
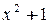Другой подход основан на построении поля комплексных чисел как подкольца кольца квадратных матриц второго порядка над полем действительных чисел.
Рассмотрим множество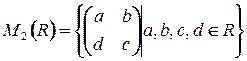 
. 
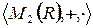- кольцо. В этом кольце выбирается подмножество 
.
Теорема 1.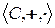 
- поле.
