III. 1.2 Инерционное звено

Звено называется инерционным, если связь между входным х(t) и выходным z(t) сигналами звена определяется дифференциальным уравнением вида

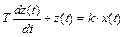. (III.1.2)

Смысл коэффициентов T и k будет пояснен позже. Такое звено называют также апериодическим, статистическим, одноемкостным, релаксационным.

Надо заметить, что этот тип звена наиболее часто встречается в практике автоматического управления. В качестве примеров инерционного звена можно назвать термопару, магнитный усилитель, двигатель постоянного тока с независимым возбуждением, генератор и т.д.

Если к (III.1.2) применить преобразование Лапласа, при нулевых начальных условиях, то получится

.

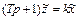Найдем отсюда передаточную функцию звена

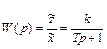. (III.1.3)

Переходная характеристика звена определиться из выражения

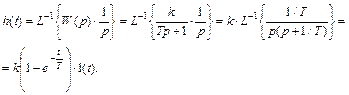
На рисунке III.6 представлены для сравнения сигналы х (t) = 1(t) и z (t) = h (t) инерционного звена

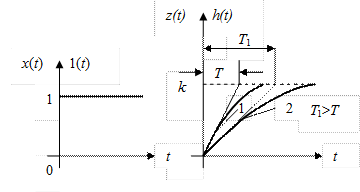
Рис. III.6 Единичный скачок и переходная

функция инерционного звена.

Из рисунка видно, что, сравнивая установившиеся значение выходного сигнала звена k и величину входного 1(t), можно сделать вывод, что параметр k в (III.1.2) есть коэффициент усиления звена. Из этого же рис. III.6. видно, что кривая 2 характеризует более замедленную, более инертную реакцию звена на единичный скачок. Для кривой 2 параметр Т ₁ (смысл которого ясен из рисунка) больше параметра Т для кривой 1.Ззначит, этот параметр может служить мерой инерционности звена. Обычно, этот коэффициент Т называют постоянной времени звена.

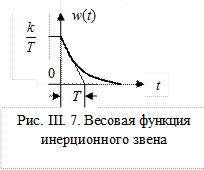
Импульсная переходная (весовая) функция звена w (t), представленная на рис. III.7, определяется следующим образом

.

Получим частотную передаточную функцию звена W (j ω), заменив в (III.1.3) р на j ω

.

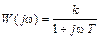Отсюда легко определяются АЧХ A(ω) и ФЧХ φ(ω)

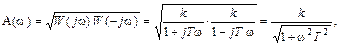
φ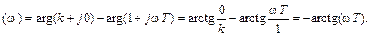

Качественный вид графиков, соответствующих вышенайденным зависимостям A(ω) и φ(ω), представлен на рис. III.8.

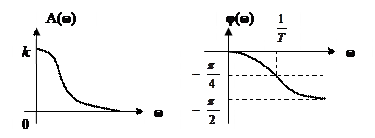
Рис.III.8 АЧХ и ФЧХ инерционного звена.

По найденным графикам A(ω) и φ(ω) на рис. III.9. построена амплитудно-фазовая характеристика инерционного звена

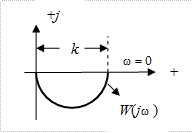
Рис. III. 9. АФХ инерционного звена.

Из выражения для АЧХ звена получим соотношение для точной ЛАЧХ

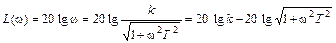. (III.1.4)

В выражении для L (ω) вычислять слагаемое 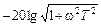для различных частот от 0 до ∞ представляет определенные неудобства. Вот если бы удалось диапазон частот 0 ≤ ω < ∞ так разбить на два (в данном конкретном случае) поддиапазона, чтобы в каждом из них кривая линия 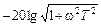была бы заменена прямой линией (асимптотой) с собственным наклоном, вычисления существенно бы упростилось.

В качестве первого участка возьмем диапазон частот, для которого 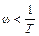или ω T <1. Тогда в выражении для асимптоты первого порядка вторым слагаемым подкоренного выражения 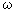² T ² можно пренебречь по сравнению с первым

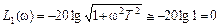
Итак, первая асимптота представляет собой прямую линию, не зависящую от часты, и проходящую по оси частот. Наклон такой асимптоты равен 0.

На втором участке рассмотрим диапазон частот, для которого 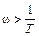или ω T >1. Тогда асимптота второго участка может быть получена, если в выражении 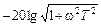пренебречь первым слагаемым подкоренного выражения по сравнению со вторым

.

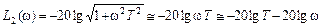Поскольку при построении ЛАЧХ по оси абсцисс частоты откладываются в логарифмическом масштабе, то вторая асимптота представляет собой уравнение прямой, зависящей от частоты ω (т.е. проходящей с некоторым наклоном к оси частот). Ниже будет показано, как определять наклон таких асимптот.

Когда же сопрягаются, т.е. становятся равными эти две асимптоты L ₁(ω) и L ₂(ω)? Очевидно, тогда, когда первое слагаемое подкоренного выражения точной кривой 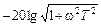становится равным второму

1= ω² T ².

Отсюда частота, при которой сопрягаются обе асимптоты, или сопрягающая частота

.

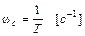Асимптоты L ₁(ω) и L ₂(ω) представляют собой совокупность прямых, приблизительно заменяющих точную кривую 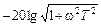(рис. III.10). На этом рисунке помимо асимптот L ₁(ω) и L ₂(ω) пунктиром показана и упомянутая точная кривая.

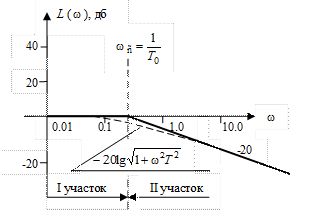
Рис. III.10. Точная ЛАЧХ 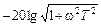и ее асимптоты.

Вернемся к выражению (III.1.4) для точной ЛАЧХ звена и построим асимптоты, приблизительно ее заменяющие.

Начинать построение ЛАЧХ рекомендуется с определения сопрягающих частот. Сопрягающих частот у ЛАЧХ будет столько, сколько звено (или САР) имеет постоянных времени. В случае инерционного звена из (III.1.3) видно, что имеется лишь одна постоянная времени Т и, значит, одна сопрягающая частота

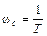
Эта сопрягающая частота делит ось частот на два участка ω < ω_c и ω > ω_c. Для более сложных звеньев или САР число постоянных времени может достигать произвольного значения m, тогда число участков будет m+1.

В случае инерционного звена рассмотрим:

I участок

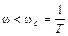или ω T <1. (III.1.5)

Выражение для асимптоты I участка L ₁(ω) получим из соотношения (III.1.4) для точной ЛАЧХ, если учтем условие (III.1.5), т.е. в подкоренном выражении члена 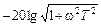пренебрежем вторым слагаемым по сравнению с первым. Тогда получится

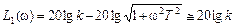
Это уравнение горизонтальной прямой (ее значение не зависит от частоты ω), проходящей при k =100 на расстоянии 20lg100=40 дб от оси абсцисс до частоты ω_c

II участок

или ω T >1. (III.1.6)

Выражение для асимптоты II участка получается аналогично предыдущему случаю, только учитывать надо условие (III.1.6) и в члене 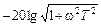следует пренебречь первым слагаемым по сравнению со вторым

.

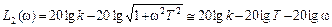Как уже говорилось выше, с учетом логарифмического масштаба по оси частот данное выражение представляет собой прямую линию, имеющий некоторый наклон к оси абсцисс. Чтобы провести эту асимптоту на графике, необходимо знать ее наклон и точку, через которую проходит данная прямая. Что касается упомянутой точки, то найти ее легко, если понять, что конец предыдущей асимптоты является началом следующей. В самом деле, если взять конец первой асимптоты, т.е. ее значение при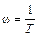

,

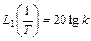и начало второй асимптоты, т.е. опять же ее значение при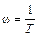

,

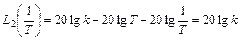то подтверждается вышеприведенное утверждение

.

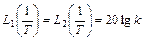Для определения наклона асимптоты к оси абсцисс найдем для частоты ω^*, относящейся ко II участку

.

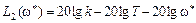Затем увеличим частоту ω^* в 10 раз (т.е. на декаду) и получим значение L ₂(10 ω^*)

.

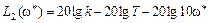Легко понять, что если взять приращение ЛАЧХ

L ₂ (10 ω^*) – L ₂ (ω^*)

и отнести его к интервалу изменения частоты, то тем самым определиться наклон асимптоты к оси частот

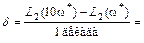
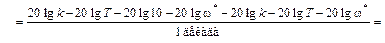
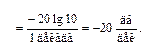
Итак, наклон второй асимптоты L ₂(ω) составляет 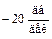, т.е. при росте частоты на 1 декаду L ₂(ω) уменьшается на 20 дб.

Вообще же, чтобы не определять каждый раз подобным способом наклоны произвольной асимптоты полезно запомнить следующее правило, наклон асимптоты к оси частот определяется коэффициентом со знаком, стоящим при члене lg ω в выражении для асимптоты. Например, если

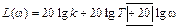
то соответствующий наклон равен 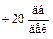, а при

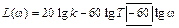
этот наклон будет .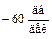

На рис. III.11 изображена ЛАЧХ инерционного звена своими асимптотами

.

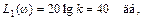
Часто ЛАЧХ звена или системы характеризуют путем обозначения наклонов ее асимптот. В данном случае эта характеристика будет выглядеть так

.

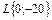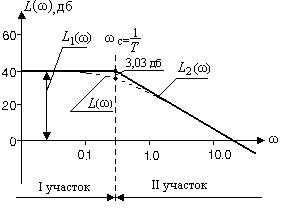
Рис. III. 11 ЛАЧХ инерционного звена.

На этом же рисунке пунктиром изображена точная ЛАЧХ L (ω) (III.1.4). Видно, что максимальная ошибка, возникающая от замены точной ЛАЧХ на асимптотическую, наблюдается на сопрягающей частоте 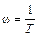и приблизительно равна 3,03 дб.

Чтобы оценить влияние параметров звена k и T на его ЛАЧХ, надо понять, что изменение k приводить к изменению 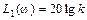. Иными словами, при изменении k первая асимптота перемещается по вертикали параллельно самой себе. Но так как конец первой асимптоты является началом второй, т.е. первая и вторая асимптоты жестко связаны, то точно такое же перемещение по вертикали будет претерпевать и вся асимптотическая ЛАЧХ.

Понятно так же, что при изменении Т меняется сопрягающая частота 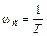. Значит, при изменении T ЛАЧХ инерционного звена будет перемещаться по горизонтали параллельно самой себе.