Звено называют колебательным, если связь между входной x (t) и выходной z (t) переменными определяется дифференциальным уравнением вида
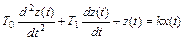 ,
,
причем корни характеристического уравнения, отвечающего этому дифференциальному уравнению
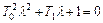 ,
,
должны быть комплексно сопряженными, т.е. должно выполнятся условие 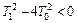 . Если это неравенство имеет противоположный знак, то корни будут вещественными и вместо колебательного звена получится последовательное соединение двух инерционных звеньев.
. Если это неравенство имеет противоположный знак, то корни будут вещественными и вместо колебательного звена получится последовательное соединение двух инерционных звеньев.
Часто дифференциальное уравнение колебательного звена записывают в ином виде, введя степень затухания (степень успокоения) ξ 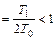 (при ξ >1 получается два инерционных звена)
(при ξ >1 получается два инерционных звена)
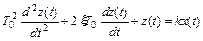 .
.
В операторной форме это уравнение может быть записано в виде
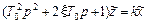 ,
,
и значит, передаточная функция звена будет такова
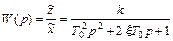 (III. 1.11)
(III. 1.11)
В качестве примера колебательно звена можно привести пассивный RLC – контур (рис. III. 24).
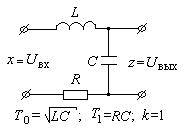
Рис. III. 24. Пример колебательного звена.
Интересен бывает частный случай колебательного звена, когда степень затухания ξ = 0, такое звено называют консервативным. Его передаточная функция получается при ξ = 0 из (III. 1.11)
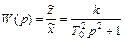 (III.1.12)
(III.1.12)
Переходная характеристика колебательного звена определяется выражением
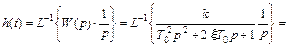
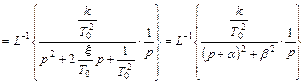
Представление выражения 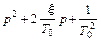 в виде
в виде 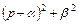 понадобилось потому, что в справочниках по операционному исчислению дается следующие стандартные выражения для обратного преобразования Лапласа
понадобилось потому, что в справочниках по операционному исчислению дается следующие стандартные выражения для обратного преобразования Лапласа
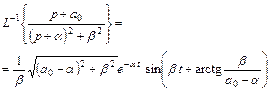 (III.1.13)
(III.1.13)
Получить введенные неизвестные коэффициенты α и β через заданные ξ и Т 0 можно из выражения
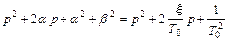 ,
,
приравняв коэффициенты при одинаковых степенях p
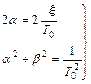 .
.
Отсюда
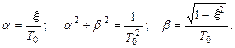 (III.1.14)
(III.1.14)
Разложим выражение в фигурных скобках для h (t) на простейшие дроби

где А1, А2, А3 – неопределенные пока коэффициенты, подлежащие определению.
Приведем к общему знаменателю правую часть этого выражения, и поскольку знаменатели слева и справа окажутся одинаковыми, приравняем числители и приведем подобные.
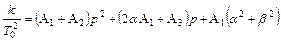 .
.
Затем, приравняв коэффициенты при одинаковых степенях переменной р, получим
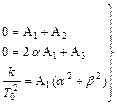 . (III.1.15)
. (III.1.15)
Из третьего равенства (III. 1.15) и (III.1.14) следует, что
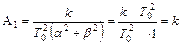
Тогда из остальных равенств (III. 1.15) найдем
А2 = – А1= – k
А3 = – 2αА1= – 2α k.
Отсюда, с учетом найденных значений для А1, А2, А3, получим, имея в виду (III. 1.13), 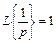 и (III.1.14)
и (III.1.14)
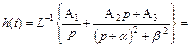
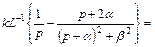
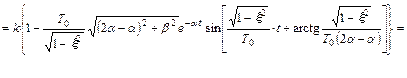
 (III.1.16)
(III.1.16)
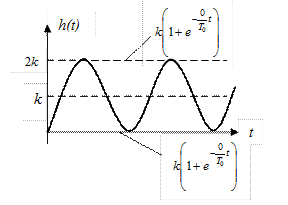
Эта переходная характеристика звена изображена на рис. III. 25.
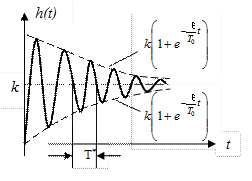
Рис. III. 25. Переходная характеристика колебательного звена.
Прямо из рисунка можно определить параметр k (коэффициент усиления звена) и Т * – период колебаний процесса
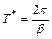 .
.
На этом же рисунке нанесены пунктиром экспоненты затухания колебаний 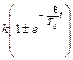 . В соответствии с этими экспонентами изменяется (здесь уменьшается) с течением времени амплитуда колебаний переходного процесса.
. В соответствии с этими экспонентами изменяется (здесь уменьшается) с течением времени амплитуда колебаний переходного процесса.
Для консервативного звена (ξ =0) экспоненты превращаются в горизонтальные линии и, следовательно, затухания колебаний не происходит (рис.III.26). это, впрочем, видно и из (III.1.16), если положить там ξ =0
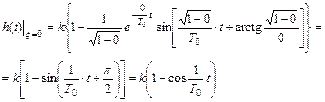
 2014-02-02
2014-02-02 1993
1993
