Оценка значимости параметров линейной регрессии и корреляции

Предпосылки применения МНК (условия Гаусса— Маркова)

1. Математическое ожидание случайного отклонения равно нулю 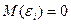для всех наблюдений. Данное условие означает, что случайное отклонение в среднем не оказывает влияния на зависимую переменную. В каждом конкретном наблюдении случайный член может быть либо положительным, либо отрицательным, но он не должен иметь систематического смещения.

2. Дисперсия случайных отклонений постоянна для любых наблюдений i и j: 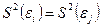. Данное условие подразумевает, что несмотря на то, что при каждом конкретном наблюдении случайное отклонение может быть либо большим, либо меньшим, не должно быть некой априорной причины, вызывающей большую ошибку (отклонение). Выполнимость данной предпосылки называется гомоскедастичностью (постоянством дисперсии отклонений). Невыполнимость данной предпосылки называется гетероскедастичностъю (непостоянством дисперсий отклонений).

3. Случайные отклонения являются независимыми друг от друга. Выполнимость данной предпосылки предполагает, что отсутствует систематическая связь между любыми случайными отклонениями. Другими словами, величина и определенный знак любого случайного отклонения не должны быть причинами величины и знака любого другого отклонения. Выполнимость данной предпосылки влечет следующее соотношение: 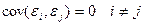. Поэтому, если данное условие выполняется, то говорят об отсутствии автокорреляции.

4. Случайное отклонение должно быть независимо от объясняющих переменных. Обычно это условие выполняется автоматически при условии, что объясняющие переменные не являются случайными в данной модели. Данное условие предполагает выполнимость следующего соотношения: .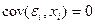

5. Модель должна быть линейной относительно параметров.

Теорема Гаусса—Маркова. Если предпосылки 1 - 5 выполнены, то оценки, полученные по МНК, обладают следующими свойствами:

1. Оценки являются несмещенными, т. е. М(b₀) = b0, М(b₁) = b₁. Это вытекает из того, что 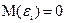и говорит об отсутствии систематической ошибки в определении положения линии регрессии.

2. Оценки состоятельны, т. к. дисперсия оценок параметров при возрастании числа наблюдений n стремится к нулю. Другими словами, при увеличении объема выборки надежность оценок увеличивается.

3. Оценки эффективны, т. е. они имеют наименьшую дисперсию по сравнению с любыми другими оценками данных параметров, линейными относительно величин у_i.

В англоязычной литературе такие оценки называются BLUE (Best Linear Unbiased Estimators) -наилучшие линейные несмещенные оценки.

Если предпосылки 2° и 3° нарушены, т. е. дисперсия отклонений непостоянна и (или) значения 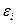связаны друг с другом, то свойства несмещенности и состоятельности сохраняются, но свойство эффективности - нет.

Наряду с выполнимостью указанных предпосылок при построении классических линейных регрессионных моделей делаются еще некоторые предположения. Например:

• объясняющие переменные не являются случайными величинами:

• случайные отклонения имеют нормальное распределение;

• число наблюдений существенно больше числа объясняющих переменных;

• отсутствуют ошибки спецификации;

• отсутствует мультиколлннеарность.

После того как уравнение линейной регрессии найдено, проводится оценка значимости (существенности) как уравнения в целом, так и отдельных его параметров.

Оценка значимости уравнения регрессии в целом дается с помощью F -критерия Фишера. При этом выдвигается нулевая гипотеза, что коэффициент регрессии равен нулю, т. е. b = 0, и, следовательно, фактор х не оказывает влияния на результат у.

Непосредственному расчету F -критерия предшествует анализ дисперсии. Центральное место в нем занимает разложение общей суммы квадратов отклонений переменной у от среднего значения на две части – «объясненную» и «остаточную» («необъясненную»):

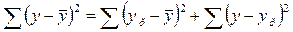(2.11)

Общая сумма Сумма квадратов Остаточная сумма

квадратов = отклонений, + квадратов

отклонений объясненная отклонений

регрессией

Общая сумма квадратов отклонений индивидуальных значений результативного признака у от среднего значения вызвана влиянием множества причин. Условно разделим всю совокупность причин на две группы: изучаемый фактор х и прочие факторы. Если фактор не оказывает влияния на результат, то линия регрессии на графике параллельна оси 0 х и = у. Тогда вся дисперсия результативного признака обусловлена воздействием прочих факторов и общая сумма квадратов отклонений совпадет с остаточной. Если же прочие факторы не влияют на результат, то у связан с х функционально и остаточная сумма квадратов равна нулю. В этом случае сумма квадратов отклонений, объясненная регрессией, совпадает с общей суммой квадратов.

Поскольку не все точки поля корреляции лежат на линии регрессии, то всегда имеет место их разброс, как обусловленный влиянием фактора х, т.е. регрессией у по х, так и вызванный действием прочих причин (необъясненная вариация). Пригодность линии регрессии для прогноза зависит от того, какая часть общей вариации признака у приходится на объясненную вариацию. Очевидно, что если сумма квадратов отклонений, обусловленная регрессией, будет больше остаточной суммы квадратов, то уравнение регрессии статистически значимо и фактор х оказывает существенное влияние на результат у. Это равносильно тому, что коэффициент детерминации r_x_у будет приближаться к единице.

Любая сумма квадратов отклонений связана с числом степеней свободы df (degrees of freedom), т.е. с числом свободы независимого варьирования признака. Число степеней свободы связано с числом единиц совокупности п и с числом определяемых по ней констант. Факторная сумма квадратов отклонений имеет число степеней свободы, равное 1. Число степеней свободы остаточной суммы квадратов при линейной регрессии составляет n – 2. Число степеней свободы для общей суммы квадратов df _общ = n – 1.

Итак, имеем два равенства:

1) 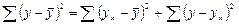(2.14)

2) n – 1 = 1 + (n – 2).

;

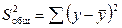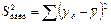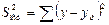Разделив каждую сумму квадратов на соответствующее ей число степеней свободы, получим средний квадрат отклонений или дисперсию на одну степень свободы S ² и вытекающую из нее стандартную ошибку S.

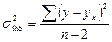
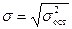Определение дисперсии на одну степень свободы приводит дисперсии к сравнимому виду. Сопоставляя факторную и остаточную дисперсии в расчете на одну степень свободы, получим величину F -отношения, т.е. критерий F:

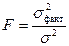(2.15)