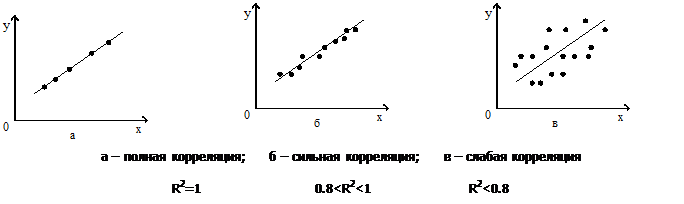
После проверки значимости каждого коэффициента регрессии обычно проверяется общее качества уравнения регрессии, которое оценивается по тому, как хорошо полученное уравнение регрессии согласуется с экспериментальными данными. Другими словами, насколько широко рассеяны точки наблюдений относительно линии регрессии. Очевидно, если все точки лежат на построенной прямой, то регрессия Y на Х идеально объясняет поведение зависимой переменной. Но в реальных условиях такая ситуация практически не встречается. Обычно поведение Y лишь частично объясняется влиянием переменной Х.
Суммарной мерой общего качества уравнения регрессии (соответствия уравнения статистическим данным) является коэффициент детерминации R2. В случае парной регрессии коэффициент детерминации будет совпадать с квадратом коэффициента корреляции. В общем случае коэффициент детерминации рассчитывается по формуле:
 следует, что
следует, что
Слагаемое 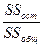 определяет долю разброса зависимой переменной, необъясненную регрессией. Тогда R2 показывает долю разброса Y, объясненную моделью регрессии.
определяет долю разброса зависимой переменной, необъясненную регрессией. Тогда R2 показывает долю разброса Y, объясненную моделью регрессии.
Из проведенных рассуждений следует, что в общем случае справедливо соотношение 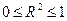 . Чем теснее линейная связь между Y и Х, тем ближе R2 к 1.
. Чем теснее линейная связь между Y и Х, тем ближе R2 к 1.
7. Интервальный прогноз для y*
Часто уравнение регрессии используют для определения прогнозного значения 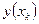 , зная значение
, зная значение 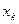 . Это делается путем подстановки в уравнение регрессии
. Это делается путем подстановки в уравнение регрессии 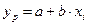 вместо х значения
вместо х значения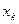 . Однако в большинстве случаев точечный прогноз дополняется интервальным. Задается уровень надежности и рассчитывается доверительный интервал для прогнозного значения y*.
. Однако в большинстве случаев точечный прогноз дополняется интервальным. Задается уровень надежности и рассчитывается доверительный интервал для прогнозного значения y*.
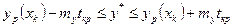
Стандартная ошибка для yp определяется по формуле
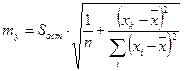
Рассмотренная формула стандартной ошибки предсказываемого среднего значения y при заданном значении xk характеризует ошибку положения линии регрессии. Величина стандартной ошибки 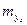 достигает минимума при
достигает минимума при 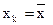 и возрастает по мере того, как «удаляется» от
и возрастает по мере того, как «удаляется» от 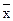 в любом направлении. Иными словами, чем больше разность между xk и
в любом направлении. Иными словами, чем больше разность между xk и 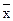 , тем больше ошибка
, тем больше ошибка  , с которой предсказывается среднее значение y для заданного значения xk. Можно ожидать наилучшие результаты прогноза, если признак-фактор x находится в центре области наблюдения x и нельзя ожидать хороших результатов прогноза при удалении xk от
, с которой предсказывается среднее значение y для заданного значения xk. Можно ожидать наилучшие результаты прогноза, если признак-фактор x находится в центре области наблюдения x и нельзя ожидать хороших результатов прогноза при удалении xk от 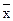 . Если же значение xk оказывается за пределами наблюдаемых значений, используемых при построении линейной регрессии, то результаты прогноза ухудшаются в зависимости от того, насколько xk откланяется от области наблюдаемых значений фактора x.
. Если же значение xk оказывается за пределами наблюдаемых значений, используемых при построении линейной регрессии, то результаты прогноза ухудшаются в зависимости от того, насколько xk откланяется от области наблюдаемых значений фактора x.
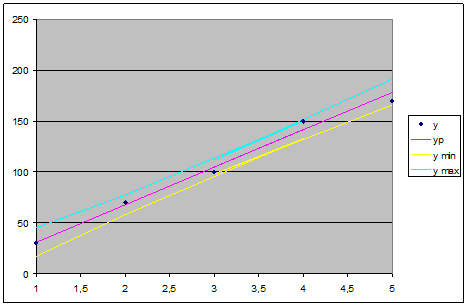
Для рассмотренного примера
| x | y | yp | (y-yp)^2 | (x-xсp)^2 | my | y min | y max |
| 31,05263 | 1,108033 | 4,5918367 | 5,4569583 | 17,0251 | 45,08017 | ||
| 67,89474 | 4,432133 | 1,3061224 | 3,7216146 | 58,32804 | 77,46144 | ||
| 141,5789 | 70,91413 | 0,7346939 | 3,3287133 | 133,0222 | 150,1357 | ||
| 104,7368 | 22,43767 | 0,0204082 | 2,7600233 | 97,64199 | 111,8317 | ||
| 178,4211 | 70,91413 | 3,4489796 | 4,9232334 | 165,7655 | 191,0766 | ||
| 104,7368 | 22,43767 | 0,0204082 | 2,7600233 | 97,64199 | 111,8317 | ||
| 141,5789 | 70,91413 | 0,7346939 | 3,3287133 | 133,0222 | 150,1357 | ||
| 3,142857 | 263,158 | 10,857143 | |||||
| x cp | y cp | SS ост | |||||
| S^2 | 52,63158 | ||||||
| S | 7,254763 |
 2014-02-02
2014-02-02 2853
2853