2014-02-02
774
В электрической цепи при параллельном соединении ветвей с R (G), L (BL), C (BC) ток определяется по формуле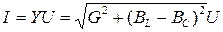 
.
Особый интерес представляет случай, когда индуктивная и емкостная реактивные проводимости равны друг другу. Тогда полная проводимость цепи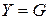 
, так как 
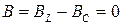, а полный ток
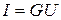
имеет минимальное значение и только активную составляющую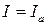 
. Следовательно, 
.
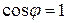Токи в ветвях с проводимостями BL и BC
; 
,
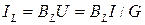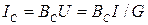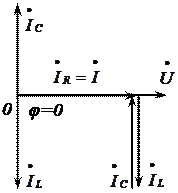то есть равны по значению (
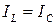) и могут превышать полный ток в цепи в 
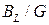раз, если 
. Векторная диаграмма токов для рассмотренного случая имеет вид
Режим цепи при параллельном соединении элементов с R, L и C, когда 
, а токи в ветвях с реактивными проводимостями IL и IC равны по значению и могут превышать полный ток цепи, называется режимом резонанса токов. Для этого режима характерно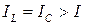 
, если ;
; 
; ;
;
; 
; 
.
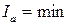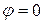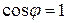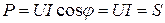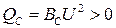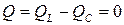В режиме резонанса токов рассматриваемая цепь ведет себя по отношению к источнику питания так, как будто она состоит только из элементов с активной проводимостью. В действительности же в параллельных ветвях L и C могут протекать токи, даже превышающие полный ток, протекающий в источнике питания. Но эти токи всегда противоположны по фазе друг другу. Это означает, что через каждую четверть периода происходит обмен энергиями между магнитным полем индуктивной катушки и электрическим полем конденсатора, который поддерживается напряжением U источника питания.
