Импульсные системы – это системы, у которых сигналы квантованы по времени. Квантование бывает по уровню и по времени (например электронные часы). Впервые такие системы появились в радиолокационных станциях в годы войны.
t=0¸Т (Чем меньше значение Т - периода дискретизации, тем ближе импульсная система к аналоговой).
Особенности импульсных систем:
1. Импульсные системы исследуются специальным математическим аппаратом.
2. Применяются при использовании микро-ЭВМ (если их исследовать учитывая квантование, то можно получить лучшее качество системы).
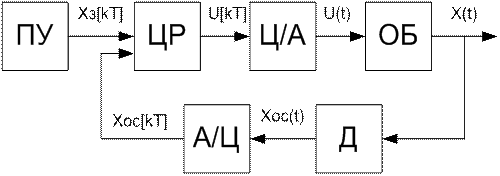
Цифровыми называются системы, в которых имеет место квантование сигналов и по времени и по уровню. При математическом описании систем, в которых применяется цифровой регулятор, выполненный в виде микропроцессорного контроллера или управляющей ЭВМ, квантованием по уровню сигналов из-за достаточно высокой разрядности можно пренебречь. В то же время квантование по времени является существенным фактором, влияющим на работу САУ. На рисунке представлена функциональная схема САУ с цифровым регулятором.
ЦР - цифровой (импульсный) регулятор,
Ц/А и А/Ц - цифро-аналоговый и аналого-цифровой преобразователи;
ОБ - объект регулирования;
Д - датчик;
ПУ - пульт управления (задающее устройство).
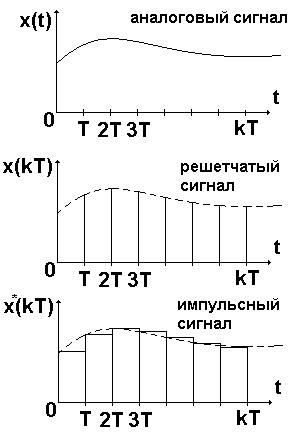
Т=const – период квантования
k - номер периода, t=0T, 1T, 2T, …, kT
t*=t/T=0, 1, 2, …, k
x[k] – относительная величина
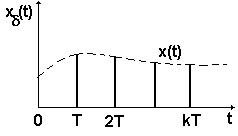
В период kT функции 1 и 2 имеют одно и тоже значение, но мы не знаем значения решетчатой функции в моменты времени между квантами. Значения импульсной функции постоянны на периоде Т, но ширина импульса может колебаться 0<=tи<=T.
Рассмотрим понятие производной по отношению к импульсным функциям.
Вообще говоря, понятие производной по отношению к импульсным системам некорректно (здесь нет и дифференциальных уравнений). Используются разностные уравнения:
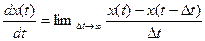 (1)
(1)
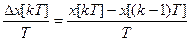 (2) Dtmin=T
(2) Dtmin=T
Запишем обобщенное разностное уравнение (n<=m):
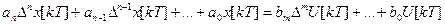 (3)
(3)
D - некоторое конечное приращение функции (d за Dt®0, D за Dt=Т).
Функция Диракка  при t=0 d(t)=¥
при t=0 d(t)=¥
d(t-kT), где k=0, 1, 2, …
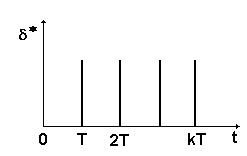
при t=2T d(t-2T)=¥
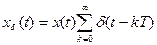 (4)
(4)
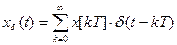 (5)=(4)
(5)=(4)
Значение функции равно ¥, но площадь криволинейной трапеции имеет значение x(t).
Импульсные системы описываются с помощью дискретного преобразования Лапласа или Z-преобразования:
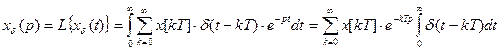
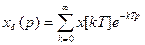 (6) – дискретное преобразование Лапласса
(6) – дискретное преобразование Лапласса
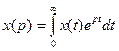 - непрерывное преобразование Лапласса
- непрерывное преобразование Лапласса
Обозначим 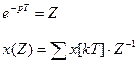 (7) - Z-преобразование
(7) - Z-преобразование
Вывод дискретной передаточной функции:
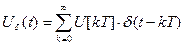 (8)
(8)
1(t)®h(t)
d(t)®v(t) 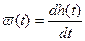
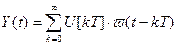 (9)
(9)
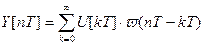 (10)
(10)
Обозначим n-k=q и подвергнем выражение (10) дискретному преобразованию Лапласса:
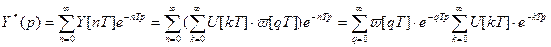 (11) (12)
(11) (12)
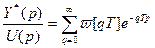 (13)
(13)
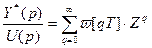 (14)
(14)
Импульсная передаточная функция определяется выражением (14), как сумма бесконечной арифметической прогрессии (прогрессия сходится, так как  ).
).
На практике используют готовые таблицы дискретного преобразования.
Таблица 1. Z-преобразование функций времени.
| x(t) | X(s) | x[nT] | X(z) |
| d(t) | d[nT] | ||
| 1(t) | 1/s | 1[nT] | z/(z-1) |
| t | 1/s2 | nT | Tz/(z-1)2 |
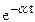
| 1/(s+a) | 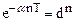
| z/(z-d)
(d=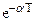 ) )
|
 2014-02-02
2014-02-02 600
600








