
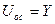
Для того, чтобы e=0 необходимо чтобы Uз=Y.
1. Все звенья системы статические, т.е. нет интегрирующих звеньев, не охваченных местной обратной связью.
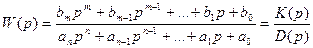
При t®¥ (установившийся режим) р®0
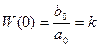 - статический коэффициент передачи звена;
- статический коэффициент передачи звена;
1.1. Разомкнутая САУ.
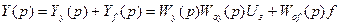
В установившемся режиме при t®¥ и р®0
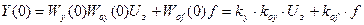
ky, koy, kf – статические коэффициенты передачи регулятора, объекта по управлению и объекта по возмущению.
Пусть f=0, тогда 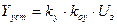
Отсюда можно найти Uз для разомкнутой системы:
Uз=0 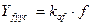
Пусть величина возмущения изменится на величину Df=f2-f1 – это вызовет отклонение выходной величины 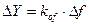 . Перейдем к относительному отклонению:
. Перейдем к относительному отклонению:
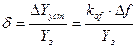
Недостатком разомкнутой системы является значительное влияние неуправляемых изменений возмущающего воздействия на выходной сигнал.
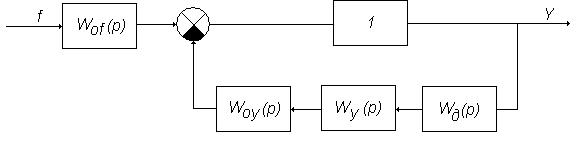
1.2. Замкнутая САУ
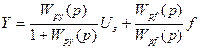
где:
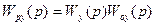 - передаточная функция разомкнутой системы по управлению,
- передаточная функция разомкнутой системы по управлению,
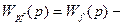 передаточная функция разомкнутой системы по возмущению.
передаточная функция разомкнутой системы по возмущению.
Выражения для передаточных функций замкнутой системы по управлению:
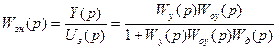

возмущению:
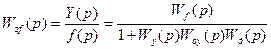
и ошибке:
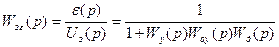
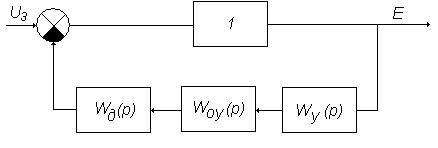
По управлению 
Для установившегося режима (при р=0):
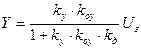
Пусть kд=1, тогда Yуст всегда меньше Yз и разность будет составлять статическую ошибку регулирования.
По возмущению:
Для оценки влияния f запишем: 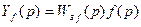
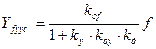
Если возмущение изменяется на величину Df, то 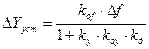
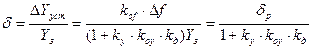
Отклонение в замкнутой САУ будет в (1+kр) раз меньше, чем в разомкнутой САУ.
Эта формула позволяет рассчитать необходимый коэффициент передачи регулятора ky для обеспечения заданной точности d.
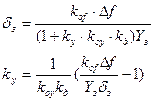
Чем больше ky, тем меньше величина d. Если ky®¥, то d®0.
По ошибке: 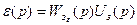
В установившемся режиме (при р=0): 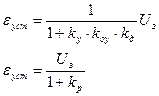
И здесь с увеличением ky значение e уменьшается, но, мы не имеем возможности бесконечно увеличивать коэффициенты, так как имеются ограничения по устойчивости. В результате, при ограниченных коэффициентах передачи ky в данной системе обязательно присутствует ошибка регулирования (e¹0).
Если задана необходимая точность регулирования e<=eз, то можно вычислить необходимый коэффициент передачи регулятора.
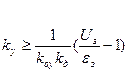
В статических системах есть однозначное соответствие управляющего воздействия на объект от величины ошибки e.
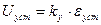
Статические системы применяют, когда допускается достаточно большая ошибка и отклонение (d>1%).
В высокоточных системах применяют регуляторы с интегрирующим звеном.
2. Астатическая система с И-регулятором.
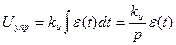
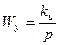
Подставим в ПФ замкнутой системы по управлению:
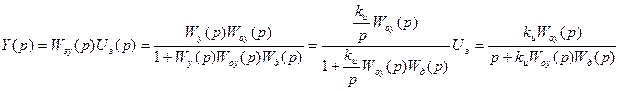
В установившемся режиме (при р=0): 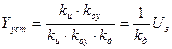
Подставим в ПФ замкнутой системы по возмущению:
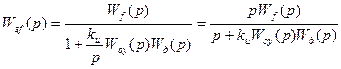
Отклонение выходного сигнала от возмущения:
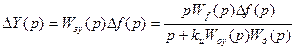
В установившемся режиме DYуст=0.
Выходной сигнал не зависит от возмущающего воздействия в установившемся режиме. Наличие интеграла в законе регулирования ведет к накоплению сигнала на выходе регулятора до тех пор, пока ошибка e не станет равной 0. При этом сигнал на выходе регулятора сохраняется на достигнутом уровне. В результате одному и тому же значению ошибки e могут соответствовать различные значения управляющего воздействия на объект Uупр (в зависимости от времени существования e), т.е. между e и Uупр отсутствует однозначное соответствие.
Такие регуляторы и системы в целом называются астатическими. Признак – наличие интегратора, не охваченного местной обратной связью. В знаменателе ПФ разомкнутой САУ есть множитель р.
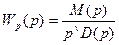
Порядок этого множителя определяет порядок астатизма системы:
v=0 – статическая САУ;
v=1 – астатизм 1-го порядка.
……………………………
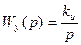
kи нельзя назвать коэффициентом передачи, так как коэффициент передачи определяется в установившемся режиме, а у интегратора его нет.
kи - называют коэффициент добротности (по скорости) интегратора и представляет собой отношение установившейся скорости изменения выходного сигнала к величине входного сигнала.
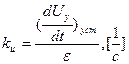
Рассмотрим поведение астатической САУ при линейно возрастающем сигнале задания, т.е. если 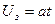
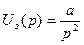
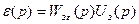
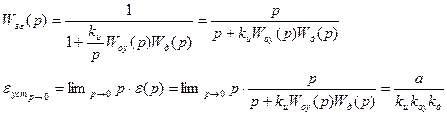
Видим, что для линейно возрастающего сигнала будет присутствовать ошибка воспроизведения:
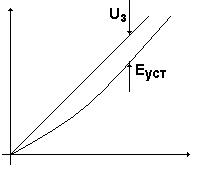
eуст®0 при kи®¥, но реально kи ограничено из условия устойчивости и поэтому обязательно будет существовать ошибка слежения (ошибка по скорости).
Можно ввести второй интегратор, тогда не будет ни статической ошибки, ни ошибки по скорости – будет ошибка по ускорению. Но введение интеграторов не является безобидной операцией. Они повышают колебательность переходных процессов, приближают границы устойчивости и могут привести к структурной неустойчивости.
 2014-02-02
2014-02-02 851
851








