Передаточные функции основных соединений звеньев

Передаточные функции основных соединений звеньев

В системах автоматического управления звенья могут находиться в самых различных сочетаниях. Однако систему любой сложности всегда можно рассматривать как совокупность трех видов соединений элементарных звеньев: последовательного, параллельного и встречно-параллельного соединений (с обратной связью).

1. Последовательное соединение.

Последовательное соединение – это такое соединение звеньев, при котором выходная величина предыдущего звена является входной величиной последующего.

Для данного рисунка x_вых1=х_вх2, х_вых2=х_вх3

По определению ПФ: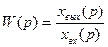

Для каждого звена можем записать:

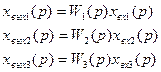
Учитывая, что x_вых1=х_вх2, х_вых2=х_вх3 исключаем из уравнений промежуточные переменные:

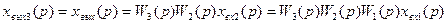
Отсюда, ПФ последовательных звеньев:

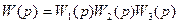
Вывод: передаточная функция группы последовательно соединенных звеньев равна произведению отдельных звеньев.

2. Параллельное соединение звеньев.

Параллельным называют соединение звеньев, при котором входные воздействия всех звеньев одинаковы, а их выходные сигналы алгебраически суммируются.

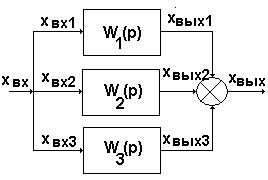
Для данного рисунка x_вх1(p)=х_вх2(p)=х_вх3(p)=х_вх(p)

x_вых(p)=х_вых1(p)+х_вых2(p)+х_вых3(p)

Для каждого звена можем записать:

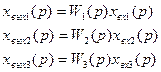
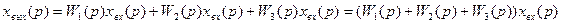
откуда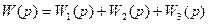

Вывод: передаточная функция группы параллельно соединенных звеньев равна сумме отдельных звеньев.

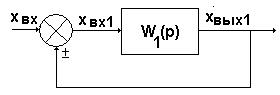
3. Встречно-параллельное соединение звеньев с обратной связью.

Встречно-параллельным называется такое соединение звеньев, при котором выходная величина звена подается обратно на его вход через другое звено. Часто такое соединение называют соединением с обратной связью (ОС). При этом звено в прямой цепи называется звеном, охваченным обратной связью, а звено, стоящее в цепи обратной связи – звеном ОС. Сигнал с выхода звена ОС может складываться или вычитаться с входным сигналом. Соответственно, ОС называется положительной или отрицательной.

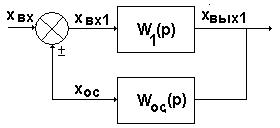
x_вх1(p)=х_вх(p)±х_ос(p)

Для каждого звена можем записать:

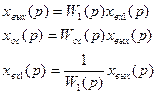
Нужно исключить переменные х_вх1 и х_ос

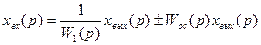
Умножаем левую и правую часть на W₁(p)

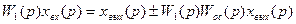
или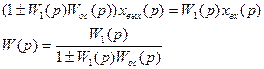

Частный случай: - единичная обратная связь.

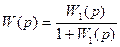
Приведем систему с неединичной обратной связью к этому виду:

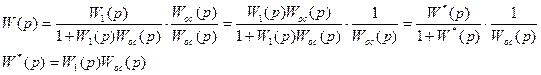
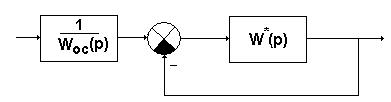
Типовые динамические звенья

При исследовании сложных технических объектов широко применяется принцип декомпозиции, то есть разбиения сложного на простые составляющие. В ТАУ широко используют разбиение сложных САУ на элементарные звенья – типовые звенья.

Типовыми называют звенья, динамика которых описывается дифференциальными уравнениями не выше 2-го порядка.

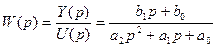
Для описания большинства реальных технических систем достаточно типовых звеньев:

1. Безинерционное-усилительное звено.

2. Интегрирующее звено.

3. Дифференцирующее звено.

4. Апериодическое звено 1-го порядка.

5. Инерционное звено 2-го порядка.

А) апериодическое звено 2-го порядка;

Б) колебательное звено 2-го порядка;

В) консервативное колебательное звено.

6. Звено запаздывания.

ФЧХ

ВЧХ

АЧХ

ДУ® ОФДУ® ПФ ®АФХ

ПХ

ФЧХ

МЧХ

АЧХ

Инерционное звено 2-го порядка.

ДУ: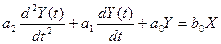

Примеры:

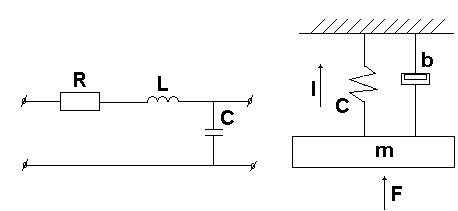
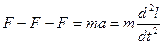
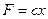
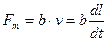
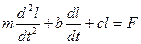
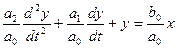
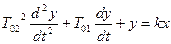
другой вид: , ,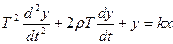

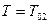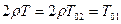r - показатель колебательности.

ОФ: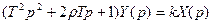

ПФ: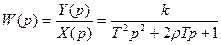

Для анализа решения рассмотрим характеристическое уравнение:

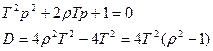
а) r>1 D>0 – разные вещественные корни;

б) r=1 D=0 – одинаковые вещественные корни;

в) 01 D– пара комплексно-сопряженных корней;

г) r=0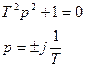

а) r>1

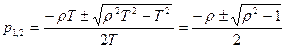
имеем пару вещественных корней, в этом случае характеристическое уравнение можно разложить на два многочлена:

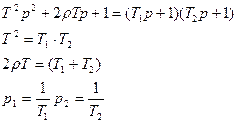
В этом случае передаточную функцию звена 2-го порядка можно представить в виде произведений ПФ 1-х порядков.

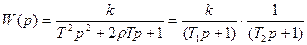
ПХ: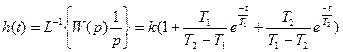

б) r=1, T₁=T₂=T

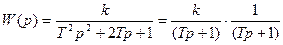
ПХ: 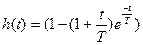- при r>=1 имеем апериодическое звено 2-го порядка.

в) 0<r<1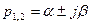

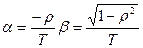
ПХ: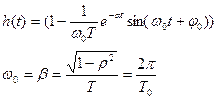

a - показатель затухания колебаний.

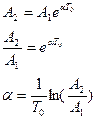
Такое звено называется колебательным звеном 2-го порядка.

г) r=0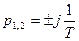

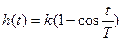
Имеем незатухающие колебания. Такое звено называется консервативным колебательным.

Частотные характеристики.

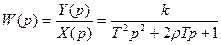
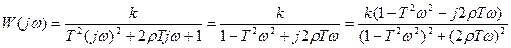
ВЧХ: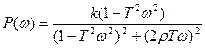

МЧХ: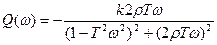

АЧХ: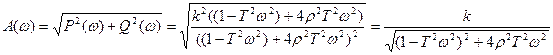

ФЧХ: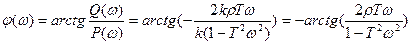

w	A(w)	j(w)
®0	k	0
w=1/T	k/2rTw	-p/2
w®¥	®0	-p

r®0 A(w)®¥