2) эмпирический (идетификация) – процесс построения модели путем измерения входных и выходных переменных.
Два условия идентификации: а) измеряемость входных и выходных переменных, б) построение модели производится в темпе функционирования объекта управления (в реальном масштабе времени). Степень адекватности модели ОУ влияет на выбор принципа управления.
4. Для синтеза систем управления применяются 3 фундаментальных принципа:
1) разомкнутого управления,
2) замкнутого (контурного) управления, обратной связи,
3) компенсации помехи.
1) Структурная схема системы управления, работающей по разомкнутому принципу.
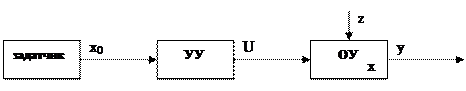 |
Задатчик вырабатывает информацию x0 о требуемом или желательном состоянии объекта управления. Сигнал x0 вырабатывается в соответствии с алгоритмом функционирования объекта управления. Устройство управления вырабатывает управление в соответствии с алготритмом управления.
2) Структурная схема системы управления, работающей по замкнутому принципу
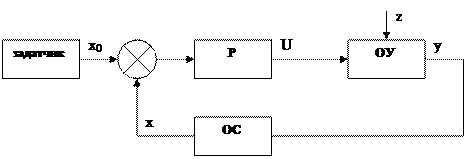 Δx=x0 - x
Δx=x0 - x
Блок обратной связи выполняет функцию градуировки сигнала Y,т.е. перевода значения величины Y в значение величины X.
Р должен вырабатывать управляющий сигнал, который изменяет состояние объекта управления так, что величина отклонения Δx→0. Выбор принципа управления производится, исходя из точности модели объекта управления.
3) Управление по возмущению (принцип компенсации помехи).
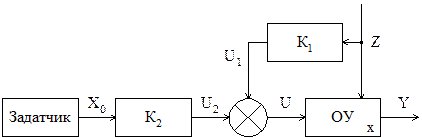
Покажем, как происходит по схеме компенсация помехи Z. Пусть задана модель одномерного ОУ:
x= KuU- KzZ (1),
где Ku и Kz известные величины (коэффициенты передачи).
Пусть блоки K1 и K2 вырабатываютуправления U1 и U2:
U1= K1Z, U2= K2x0, U=U1+U2 (2)
Значения коэффициентов K1 и K2 пока не известно. Подставим выражение (2) в уравнение (1)
X= KuK2x0+ KuK1Z- KzZ (3)
Выберем коэффициенты K1 и K2 равными 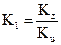 ,
, 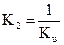 . Подставим коэффициенты K1 и K2 в выражение (3):
. Подставим коэффициенты K1 и K2 в выражение (3):
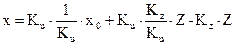
После сокращения получаем x=x0.
Это значит, выбирая соответствующим образом блоки K1 и K2, можно компенсировать помеху Z и получить состояние X объекта, равное требуемому x0.
Приведем примеры СУ, работающих в соответствии с рассмотренными принципами управления.
1) Пример разомкнутой СУ.
Объектом управления является механизм перемещения робота. Исполнительным устройством ОУ является шаговый двигатель (ШД). Если подать в обмотку ШД импульс тока, то двигатель переместит механизм на величину Δl, если подать в обмотку ШД последовательно n импульсов тока, то механизм переместится на величину nΔl. Величину Δl называют “ценой” импульса. Задатчик вырабатывает значение переменной x0, обозначающей расстояние, которое должен пройти механизм робота. УУ в соответствии с алгоритмом управления определяет 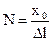 - число импульсов, которое необходимо последовательно подать в обмотку ШД, и формирует эту последовательность в виде управляющего воздействия U. После воздействия последнего импульса механизм окажется в состоянии x≈x0. Адекватность математической модели ОУ (x=NΔl) зависит от точности величины Δl. Точность определяется значением составляющих вектора Z (трение, люфт и др.). Переменная Y служит для индикации пути, пройденного механизмом.
- число импульсов, которое необходимо последовательно подать в обмотку ШД, и формирует эту последовательность в виде управляющего воздействия U. После воздействия последнего импульса механизм окажется в состоянии x≈x0. Адекватность математической модели ОУ (x=NΔl) зависит от точности величины Δl. Точность определяется значением составляющих вектора Z (трение, люфт и др.). Переменная Y служит для индикации пути, пройденного механизмом.
2) Пример СУ, работающей по принципу компенсации помехи.
Объектом управления является летательный аппарат (ЛА). Задатчик вырабатывает информацию x0 о требуемой скорости полета ЛА. Составляющая вектора Z – скорость порывов ветра и вырабартывает управление U1, которое в сумме с управлением U2 воздействует на двигатель ЛА, увеличивая или уменьшая скорость ЛА. Необходимо отметить, что математическая модель ОУ можно представить выражением x=ƒ(u), где ƒ – известная функция, её адекватность гарантируется хорошо организованной профилактикой двигателя ЛА.
На основании приведенных примеров нужно высказать очень важные положения о применении принципа разомкнутого управления и принципа компенсации помех:
1) жесткое требование к адекватности математической модели ОУ,
2) переменная Y используетс только для индикации состояния ОУ.
3) Пример замкнутой системы.
Объект управления – генератор постоянного тока Г, который изменяет напряжение Uвых при изменении тока iв в обмотке возбуждения ОВ по закону Uвых=ki iв , где ki=const. Это математическая модель ОУ, в которой Uвых играет роль одной из составляющих вектора 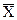 , а iв – роль одной из составляющих вектора U. Задатчиком служит источник напряжения U0, который выполняет роль переменной x0, изображенной на структурной схеме. Роль переменной Y играет напряжение Uy=Uвых ku, снимаемое с сопротивления R. Роль блока обратной связи и сумматора образует цепь, состоящая из сопротивления R, источника U0 и входа усилителя. В этой цепи источники напряжений U0 и U включены встречно, так что на входе усилителя создается напряжение Δx= U0 – Uy. Усилитель играет роль регулятора R, который вырабатывает управление U=sign Δx. Сигнал U поступает в обмотку двигателя Д, ось которого связана с ось движка потенциометра Rог. В зависимости от знака Δx, двигатель увеличивает или уменьшает значение величины Rог.
, а iв – роль одной из составляющих вектора U. Задатчиком служит источник напряжения U0, который выполняет роль переменной x0, изображенной на структурной схеме. Роль переменной Y играет напряжение Uy=Uвых ku, снимаемое с сопротивления R. Роль блока обратной связи и сумматора образует цепь, состоящая из сопротивления R, источника U0 и входа усилителя. В этой цепи источники напряжений U0 и U включены встречно, так что на входе усилителя создается напряжение Δx= U0 – Uy. Усилитель играет роль регулятора R, который вырабатывает управление U=sign Δx. Сигнал U поступает в обмотку двигателя Д, ось которого связана с ось движка потенциометра Rог. В зависимости от знака Δx, двигатель увеличивает или уменьшает значение величины Rог.
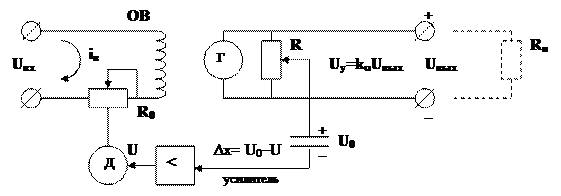 |
Если Uвых возврастает, то и Uy также возврастает, R0 увеличивается, iв уменьшается и Uвых уменьшается.
 2014-02-02
2014-02-02 502
502








