2014-02-02
779
Запишем уравнение для непрерывного ПИД-регулятора:
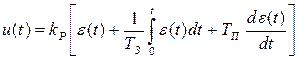. (6.12)
Для малых шагов дискретизации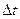 
- это уравнение можно преобразовать в разностное уравнение, состоящее в замене производной левой разностью первого порядка, а интеграл суммой. Операция интегрирования может быть заменена численным интегрированием либо по методу прямоугольников, либо по методу трапеций.
При использовании метода прямоугольников имеем, что:
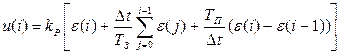. (6.13)
Выражение (6.13) представляет собой не рекуррентный алгоритм управления, в котором для формирования суммы необходимо помнить все предыдущие значения сигнала ошибки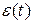 
. Поскольку каждый раз значение 
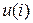вычисляется заново, этот метод называется “позиционным”.
Для получения рекуррентного алгоритма вычтем из уравнения (6.13) уравнение вида:
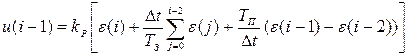. (6.14)
В итоге имеем, что
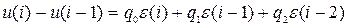, (6.15)
где
; 
; 
.
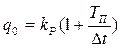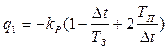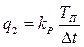В этом алгоритме управления вычисляется только приращение управляющего воздействия:
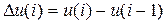, (6.16)
поэтому этот алгоритм управления называется “скоростным”.
Если интегрирование осуществлять по методу трапеций, то
|
|
|
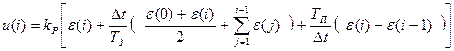. (6.17)
Вычтя из него выражение для (i-1)-го шага получим следующий “скоростной” алгоритм управления:
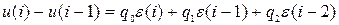, (6.18)
где
; 
; 
.
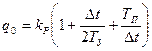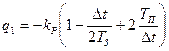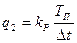Аналогичными рассуждениями можно получить разностные уравнения для других типовых регуляторов.
