Главное достоинство и удобство z-преобразования заключается в том, что сама запись z-изображения (6.7) указывает простой способ выполнения прямого и обратного z-преобразований

1) Чтобы по известной функции времени 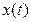найти её z-изображение, необходимо лишь каждое дискретное значение 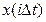умножить на 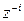, а затем свернуть получившийся степенной ряд в конечную сумму.

2) Чтобы по известному изображению 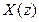найти соответствующий сигнал 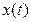, необходимо представить изображение 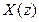в виде степенного ряда по убывающим степеням 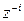, получающиеся при этом числовые коэффициенты ряда и есть дискретные значения 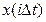сигнала .

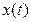Свойства z-преобразования аналогичны свойствам непрерывного преобразования Лапласа. Приведем основные из них:

1. Свойство линейности

.

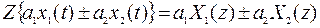1. Теорема о начальном значении оригинала:

.

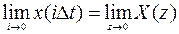1. Теорема о конечном значении оригинала:

.

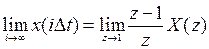1. Теорема запаздывания:

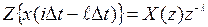. (6.8)

Соотношение (6.8) показывает, что умножение на 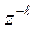соответствует задержке дискретного сигнала на l интервалов дискретизации.

Дискретной передаточной функцией называется отношение z-изображения выходной переменной к z-изображению входной переменной при нулевых начальных условиях:

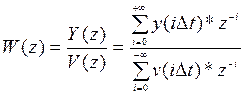, (6.9)

т.е.

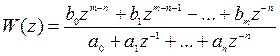, (6.10)

где 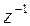- есть временная задержка на один шаг дискретизации.

Дискретные передаточные функции можно непосредственно получить по непрерывным передаточным функциям :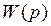

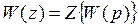. (6.11)

с использованием таблиц соответствия. Этот способ получения 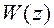является точным, однако достаточно трудоемким для САУ высокого порядка. Поэтому в практических расчетах ЦСУ используется приближенный метод получения 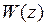через 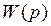, называемый методом подстановок. Самостоятельно получить разностные уравнения и 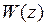для всех типовых динамических звеньев.