Параллельный способ обмена информацией.
Передача информации параллельным способом обеспечивает max возможное быстродействие схемы, но требует затрат оборудования пропорциональных разрядности передаваемого кода.
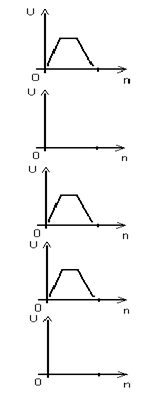 |
Целью синтеза устройств «жёсткой» логики является схемная реализация технического задания на создание устройства, обеспечивающего min аппаратных затрат и max быстродействие схемы.
Цель достигается составлением конкретной системы логических уравнений, представленных в одной из совершенных нормальных форм; минимизацией системы с учетом выбранного критерия, соответствующего цели синтеза; обоснованием выбора элементной базы и модификацией минимизированной системы, уравнений в соответствии с этим выбором; графическим представлением схемной реализации.
Пример:
Синтезировать корабельный автомат включения внутреннего освещения, работающей от системы датчиков: датчиков времени, регулируемых для каждого светового пояса, датчиков освещенности.
1 этап синтеза: формализация условий работы устройства «жёсткой» логики с использованием таблиц истинности.
x - контроль исправности осветительной сети;
y - выход датчика времени;
z - выход датчика освещенности;
x = 1- сеть исправна;
x = 0 – сеть отключена;
y = 1 - сработал датчик времени;
y = 0 – датчик не работает;
z = 0 – датчик выключен;
z = 1 – датчик включен;
F(x,y,z) - выходная функция автомата.
Таблица истинности:
| ЧИСЛОВОЙ ЭКВИВАЛЕНТ | x y z | F(x,y,z) |
| 0 0 0 0 0 1 0 1 0 0 1 1 1 0 0 1 0 1 1 1 0 1 1 1 |
2 этап синтеза: запись нормальных форм логических функций.
СДНФ: минтерм (конституент 1)
СКНФ: макстерм (конституент 0)
F(x,y,z) = (x &`y & z)Ú(x & y &`z)Ú(x & y & z) = ((x & z)&(`y Ú y))Ú(x & y &`z) = (x & z)Ú(x & y &`z)
3 этап синтеза: минимизация логических функций. Возможно использование аналитического и графо-аналитического способов. Первое требует преобразование нормальных форм с целью выделения тождественно истинных высказываний.
Для однозначности и сравнимости результатов минимизации логических функций рекомендуется использовать графо-аналитические методы, например диаграмму Вейча:
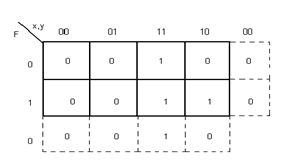 |
Fmin(x,y,z) = (x & y)Ú(x & z)
4 этап синтеза: обоснование выбора элементной базы.
Задача: Составить таблицу логических функций двух булевых переменных x, y и записать аналитические выражения для каждой функции, используя связки &,Ú,Ø.
| x | y | f1 | f2 | f3 | f4 | f5 | f6 | f7 | f8 | f9 | f10 | f11 | f12 | f13 | f14 | f15 | f16 |
f1 = 0 - логическая константа 0
f2 = x & y - конъюнкция
f3 = Ø(x®y) = Ø(ØxÚy) - отрицание прямой импликации
f4 = x - антецедент
f5 = Ø(y®x) = Ø(ØyÚ x) - отрицание обратной импликации
f6 = y - консеквент
f7 = x Å y = x mod 2 y - сложение по модулю 2
f8 = x Ú y - дизъюнкция
f9 = x¯y = Ø(x Ú y) - стрелка Пирса
f10 = x~y = (Øx &Øy)Ú(x & y) - эквивалентность
f11 = Øy - отрицание консеквента
f12 = y®x - обратная импликация
f13 = Øx - отрицание антецедента
f14 = x®y - импликация
f15 = x/y = Ø(x & y) - штрих Шеффера
f16 = 1 - логическая константа 1
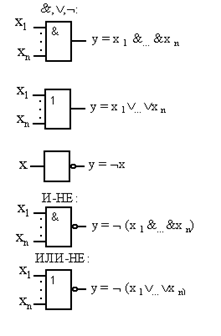 |
5 этап синтеза: графическое представление синтезированной схемы.
f(x,y,z)=(x & y)Ú(x & z) = Ø(Ø((x & y) Ú (x & z))) = Ø(Ø(x & y)&Ø(x & z)) (2)
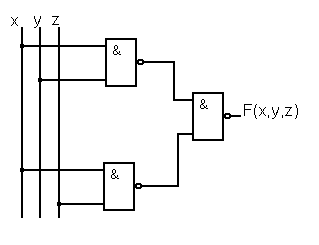 |
 2014-02-02
2014-02-02 583
583








