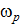Лекция 9. Свободные незатухаюшие колебания. Энергия и импульс гармонического осциллятора. Фазовая траектория. Уравнение колебаний физического маятника. Квазиупругая сила. Свободные затухающие колебания. Декремент и логарифмический декремент колебаний. Добротность колебательной системы. Вынужденные колебания. Механический резонанс.
Лекция 8. Уравнение гармонических колебаний. Графическое изображение гармонических колебаний методом векторных диаграмм. Сложение гармонических колебаний одного направления равных и близких частот. Сложение взаимно перпендикулярных гармонических колебаний равных и кратных частот.
Лекция 6-7. Работа и кинетическая энергия. Консервативные силы. Работа в потенциальном поле. Потенциальные энергии тяготения и упругих деформаций. Связь между потенциальной энергией и силой. Закон изменения механической энергии. Закон сохранения механической энергии.
Работа и кинетическая энергия
1. Работа это скалярная величина в частном случае равная произведению силы на перемещение тела, к которому приложена эта сила.
Для вычисления работы A12 в общем случае рассмотрим перемещение тела по произвольной траектории из точки 1 в точку 2. При элементарном перемещении тела вдоль траектории 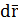 под действием силы
под действием силы 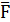 совершается элементарная работа
совершается элементарная работа
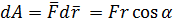 где
где 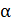 – угол между векторами
– угол между векторами 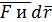 . Работу можно вычислить просуммировав все работы dA -
. Работу можно вычислить просуммировав все работы dA - 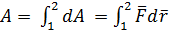
Например, работа в однородном поле силы тяжести:

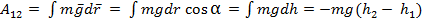
Работа во вращательном движении:
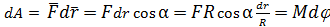 где - M момент силы,
где - M момент силы, 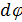 - элементарный угол поворота.
- элементарный угол поворота.
Теорема об изменении кинетической энергии
Умножим уравнение динамики тела на элементарное перемещение 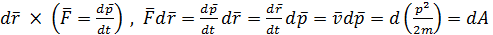
Или 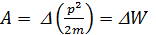 работа силы над телом равно приращению его кинетической энергии
работа силы над телом равно приращению его кинетической энергии 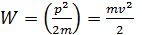
Кинетическая энергия во вращательном движении рассчитывается, как сумма кинетических энергий, составляющих тело материальных точек mi:
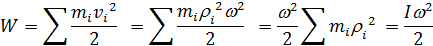
Кинетическая энергия тела массы m при плоском движении, равна сумме кинетических энергий вращательного движения относительно оси проходящей через центр масс и поступательного движения материальной точки массы m, движущейся со скоростью 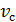 .
.
Рассмотрим классификацию сил в зависимости от их способности совершать работу. Если в каждой точке пространства на тело действует сила, то говорят что задано поле сил.
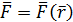
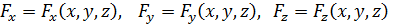
Поля бывают потенциальные и непотенциальные, силы соответственно консервативные и неконсервативные.
 Консервативные силы, это силы работа которых не зависит от от траектории движения, а зависит только от начального и конечного положения тела.
Консервативные силы, это силы работа которых не зависит от от траектории движения, а зависит только от начального и конечного положения тела.
 |
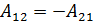
Отсюда следует, что работа сил по замкнутой траектории равна 0.
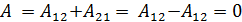
В таком силовом поле можно ввести понятие потенциальной энергии, как способности тела совершать работу над другими телами. Изменение потенциальной энергии при переходе из точки 1 в точку 2 равно работе совершенной полем над телом.
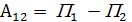 или для бесконечно малого перемещения
или для бесконечно малого перемещения
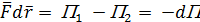
Чтобы рассчитать значение потенциальной энергии в каждой точке, необходимо произвести нормировку поля, т.е. выбрать точку пространства, в которой потенциальная энергия равна 0, например, точку 1. 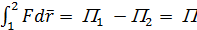
Таким образом, вместо векторного потенциального поля 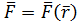 достаточно задать скалярное поле потенциальной энергии.
достаточно задать скалярное поле потенциальной энергии.
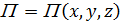
Связь между полем консервативных сил и потенциальной энергией
Если задано поле сил, то выбрав 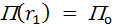 ,
,
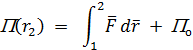
Пусть задано поле потенциальной энергии 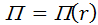
Найдем 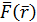 .
.
Для бесконечно малого перемещения 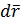

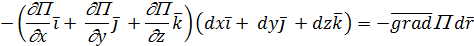
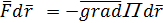 учитывая, что равенство должно выполняться при любых
учитывая, что равенство должно выполняться при любых 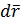 , получим
, получим 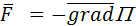
В случае одномерного поля:
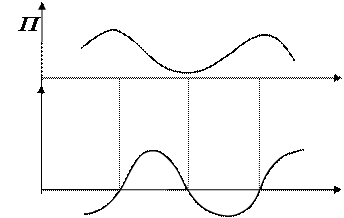
Потенциальная энергия поля силы тяжести

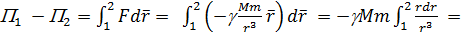
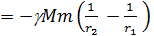
Поскольку 
Потенциальная энергия квазиупругой силы:
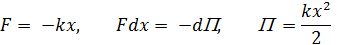
При вычислении потенциальной энергии механической системы необходимо введение понятия потенциальной энергии взаимодействия - это энергия i-го тела в силовом поле j- го 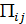 или наоборот
или наоборот 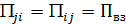 . Эта энергия принадлежит обоим телам.
. Эта энергия принадлежит обоим телам.
Тогда потенциальная энергия 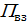 механической системы, состоящей из N тел может быть получена как сумма энергий всех тел.
механической системы, состоящей из N тел может быть получена как сумма энергий всех тел.
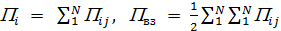
Коэффициент ½ вводится в связи с тем, что потенциальная энергия взаимодействия i-го и j-го тела учитывается при таком суммировании дважды.
Теорему об изменении кинетической энергии можно записать с использованием понятия потенциальной энергии:
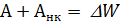 , где
, где 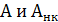 - работа консервативных и неконсервативных сил. Неконсервативные силы
- работа консервативных и неконсервативных сил. Неконсервативные силы
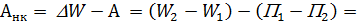
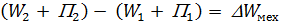 , где
, где 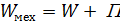
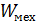 - механическая энергия, равна сумме потенциальной и кинетической энергии.
- механическая энергия, равна сумме потенциальной и кинетической энергии.
Теорема об изменении механической энергии
Для каждого из тел механической системы запишем
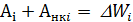 где -
где - 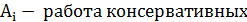 внешних и внутренних сил над i-м телом,
внешних и внутренних сил над i-м телом, 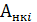 - работа неконсервативных внешних и внутренних сил над i-м телом,
- работа неконсервативных внешних и внутренних сил над i-м телом, 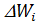 - приращение кинетической энергии i-го тела.
- приращение кинетической энергии i-го тела.
Просуммируем систему уравнений и с учетом
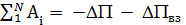 ,
, 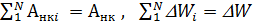 получим:
получим: 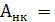
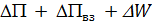 =
= 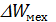
Работа неконсервативных сил механической системы равна приращению механической энергии этой системы.
Закон сохранения механической энергии
Если в механической системе работа неконсервативных сил, кА внутренних, так и внешних, равна 0, то механическая энергия остается неизменной 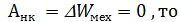
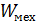 = const
= const
В частном случае если внешние неконсервативные силы системы равны 0, то такая система называется замкнутой или изолированной. Если отсутствуют также внутренние неконсервативные силы то полная энергия системы остается неизменной.
Колебаниями называется периодический процесс описываемый функцией со следующими свойствами
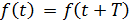 где T - период колебаний.
где T - период колебаний.
Частным случаем колебаний являются гармонические колебания
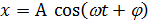
Гармонические колебания удобно представлять методом векторной диаграммы, как проекцию вращающегося вектора
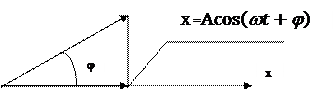 |
Сложение колебаний равных частот методом векторной диаграммы:
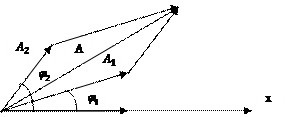
По теореме косинусов
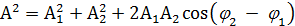
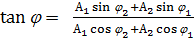
Сложение колебаний близких частот
Пусть тело участвует одновременно в двух колебаниях 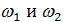 частоты которых близки
частоты которых близки 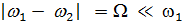
Пусть 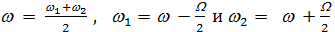
Результирующее колебание можно записать:
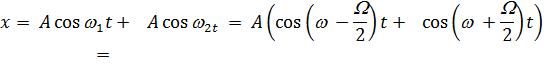
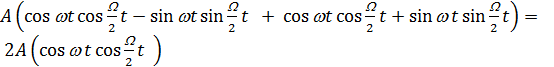
Это колебание с частотой 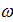 , модулированное низкой частотой
, модулированное низкой частотой  , такие колебания называются биением.
, такие колебания называются биением.
|
|
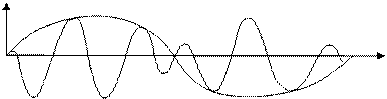
Сложение взаимно перпендикулярных колебаний равных и кратных частот.
Пусть уравнения колебаний имеют вид:
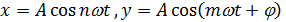
Соотношение частот этих колебаний равно 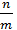
В зависимости от этого соотношения тело движется по замкнутой траектории, которая зависит от соотношения фаз 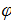 между ними:
между ними:
|
|
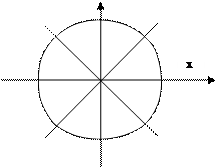 |
|
|
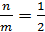
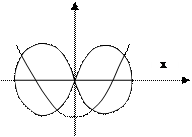 |
|
|
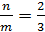
 |
Пример:
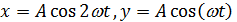
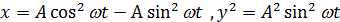
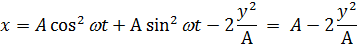
Т.е. траектория – парабола.
Свободные незатухающие колебания-
Это колебания в поле квазиупругих сил 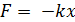
Уравнение движения 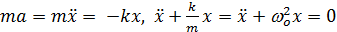
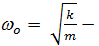 собственная частота незатухающих колебаний.
собственная частота незатухающих колебаний.
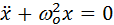 обобщенное уравнение незатухающих колебаний.
обобщенное уравнение незатухающих колебаний.
Решение этого уравнения:
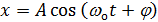
Скорость тела 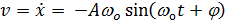
Ускорение 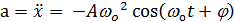
Механическая энергия колеблющегося тела:
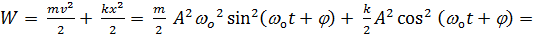
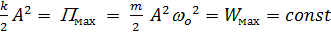
Физический маятник
- это произвольное физическое тело способное свободно вращаться относительно горизонтальной оси в поле силы тяжести. Ось вращения проходит через точку О, центр тяжести тела точка С. Расстояние от точки С до оси вращения равно d.


|
|

 неподвижной оси
неподвижной оси
|
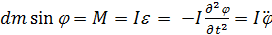
|

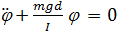
|
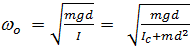
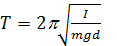
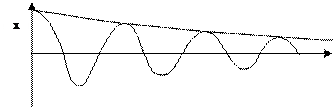
Свободные затухающие колебания
- это колебания под действием квазиупругих сил и вязкой силы трения, пропорциональной скорости 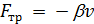 . Тогда уравнение движения:
. Тогда уравнение движения:
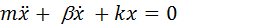
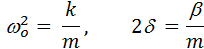
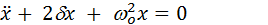
Решение данного уравнения:

Начальная амплитуда колебаний А и начальная фаза колебаний 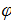 определяются начальными условиями, т.е. начальной координатой x
определяются начальными условиями, т.е. начальной координатой x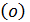 и начальной скоростью
и начальной скоростью 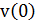 .
.
Т.е. затухающие колебания, это гармонические колебания с частотой 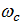 , амплитуда которых убывает со временем по экспоненциальному закону
, амплитуда которых убывает со временем по экспоненциальному закону 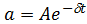 .
.
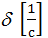 - коэффициент затухания, характеризует затухание колебаний за единицу времени.
- коэффициент затухания, характеризует затухание колебаний за единицу времени.
Декремент колебаний 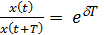 - характеризует затухание за период колебаний T.
- характеризует затухание за период колебаний T.
Логарифмический декремент колебаний 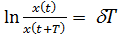
В случае 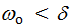 , имеет место апериодическое движение при котором тело экспоненциально приближается к точке равновесия и проходит через точку равновесия в процессе движения не более одного раза
, имеет место апериодическое движение при котором тело экспоненциально приближается к точке равновесия и проходит через точку равновесия в процессе движения не более одного раза 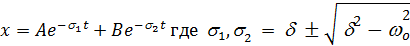
Представление колебаний посредством функции комплексной переменной с использованием формулы Эйлера 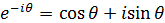 ,
,
связывающую экспоненциальную и тригонометрическую форму представления комплексного числа.
Тогда 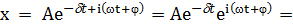
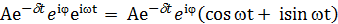
Где - 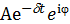 - комплексная амплитуда, в которой содержится информация об амплитуде и фазе.
- комплексная амплитуда, в которой содержится информация об амплитуде и фазе.
Действительная часть этого выражения
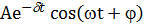 - совпадает с уравнением затухающих колебаний.
- совпадает с уравнением затухающих колебаний.
Вынужденные колебания
- это колебания в поле квазиупругих сил под действием силы вязкого трения и внешней гармонической вынуждающей силы.
Вынуждающая сила – 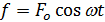 или
или 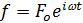
Уравнение движения 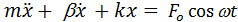
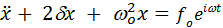
Решение этого уравнения будет суперпозицией двух решений:
- общее решение уравнения без правой части – собственные затухающие колебания,
- частное решение уравнения с правой частью – вынужденные установившееся колебания постоянной амплитуды частотой вынуждающей силы 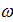 .
.
За время равное 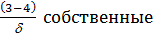 колебания затухают и остаются только вынужденные, т.е. переходный процесс.
колебания затухают и остаются только вынужденные, т.е. переходный процесс.
Решение для вынужденных колебаний ищем в виде:
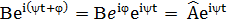 - подставим в уравнение
- подставим в уравнение
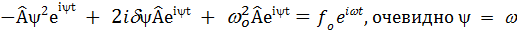
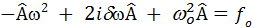

Выделим амплитуду и фазу колебаний
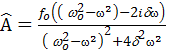
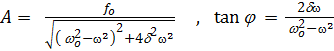
Исследуем полученные выражения:
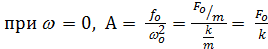 - статическое смещение.
- статическое смещение.
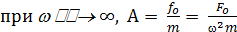 - смещение под действием вынуждающей силы в свободном пространстве.
- смещение под действием вынуждающей силы в свободном пространстве.
Найдем максимум амплитуды:
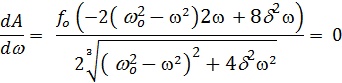
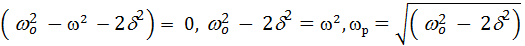
Резонансом называется достижение амплитудой вынужденных колебаний максимального значения при частоте 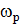 . При уменьшении коэффициента затухания резонансная частота
. При уменьшении коэффициента затухания резонансная частота 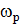 стремится к собственной частоте незатухающих колебаний
стремится к собственной частоте незатухающих колебаний 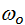 .
.
Амплитуда в точке резонанса равна:





|
|
|

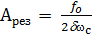
Фаза колебаний j меняется на p при изменении частоты вынуждающей силы от 0 до  . Если коэффициент затухания
. Если коэффициент затухания 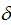 стремится к 0, то при прохождении собственной частоты незатухающих колебаний
стремится к 0, то при прохождении собственной частоты незатухающих колебаний 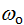 фаза колебаний j меняется на p скачкообразно.
фаза колебаний j меняется на p скачкообразно.
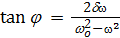
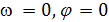
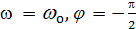
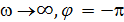
 |
Добротность D характеризует способность колебательной системы сохранять состояние свободных колебаний – D соотношение между резонансной амплитудой 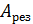 и статичеcким смещением
и статичеcким смещением 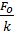 .
.
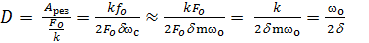
Чем больше добротность тем больше резонансная амплитуда.
 2014-02-02
2014-02-02 389
389