Свойства матриц P и Q

Для любого 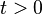матрица 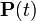обладает следующими свойствами:

1. Матричные элементы 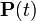неотрицательны: 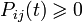(неотрицательность вероятностей).

2. Сумма элементов в каждой строке 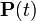равна 1: 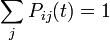(полная вероятность), то есть матрица 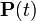является стохастической справа (или по строкам).

3. Все собственные числа матрицы 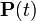не превосходят 1 по абсолютной величине: 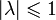. Если 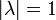, то .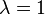

4. Собственному числу 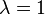матрицы 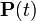соответствует, как минимум, один неотрицательный левый собственный вектор-строка (равновесие): .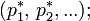

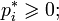
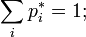
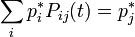5. Для собственного числа 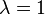матрицы 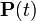все корневые векторы являются собственными, то есть соответствующие жордановы клетки тривиальны.

Матрица 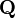обладает следующими свойствами:

1. Внедиагональные матричные элементы 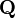неотрицательны: .

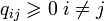2. Диагональные матричные элементы 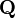неположительны: .

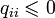3. Сумма элементов в каждой строке 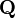равна 0: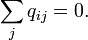

4. Действительная часть всех собственных чисел 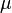матрицы 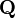неположительна: 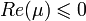. Если , то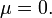

5. Собственному числу 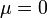матрицы 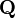соответствует, как минимум, один неотрицательный левый собственный вектор-строка (равновесие):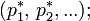

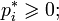
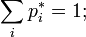
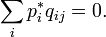
6. Для собственного числа 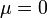матрицы 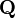все корневые векторы являются собственными, то есть соответствующие жордановы клетки тривиальны.