

Рис. Примеры графов переходов для цепей Маркова: a) цепь не является слабо эргодической (не существует общего стока для состояний 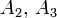 ); b) слабо эргодическая, но не эргодическая цепь (граф переходов не является ориентированно связным) c) эргодическая цепь (граф переходов ориентированно связен).
); b) слабо эргодическая, но не эргодическая цепь (граф переходов не является ориентированно связным) c) эргодическая цепь (граф переходов ориентированно связен).
Рассмотрим цепи Маркова с тремя состояниями и с непрерывным временем, соответствующие графам переходов, представленным на рис. В случае (a) отличны от нуля только следующие недиагональные элементы матрицы интенсивностей — 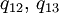 , в случае (b) отличны от нуля только
, в случае (b) отличны от нуля только 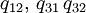 , а в случае (c) —
, а в случае (c) — 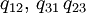 . Остальные элементы определяются свойствами матрицы
. Остальные элементы определяются свойствами матрицы 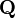 (сумма элементов в каждой строке равна 0). В результате для графов (a), (b), (c) матрицы интенсивностей имеют вид:
(сумма элементов в каждой строке равна 0). В результате для графов (a), (b), (c) матрицы интенсивностей имеют вид: 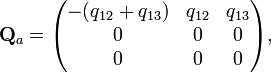
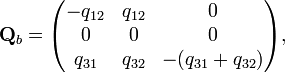
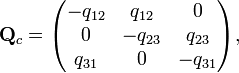
 2014-02-02
2014-02-02 547
547








