2014-02-02
396
Для основного кинетического уравнения существует богатое семейство выпуклых функций Ляпунова — монотонно меняющихся со временем функций распределения вероятностей. Пусть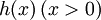 
— выпуклая функция одного переменного. Для любого положительного распределения вероятностей (
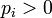) определим функцию Моримото 
:
.
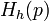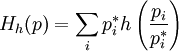Производная 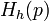по времени, если 
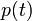удовлетворяет основному кинетическому уравнению, есть
.
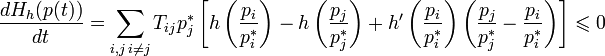Последнее неравенство справедливо из-за выпуклости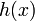 
.
Примеры функций Моримото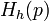
, 
;
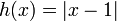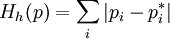эта функция — расстояние от текущего распределения вероятностей до равновесного в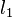 
-норме. Сдвиг по времени является сжатием пространства вероятностных распределений в этой норме. (О свойствах сжатий см. статью Теорема Банаха о неподвижной точке.)
, 
;
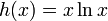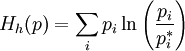эта функция — (минус) энтропия Кульбака (см. Расстояние Кульбака — Лейблера). В физике она соответствует свободной энергии, деленной на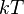 
(где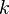 
— постоянная Больцмана, 
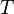— абсолютная температура):
если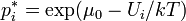 
(распределение Больцмана), то
.
, 
;
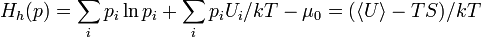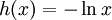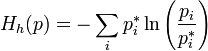эта функция — аналог свободной энергии для энтропии Бурга, широко используемой в обработке сигналов:
, 
;
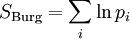
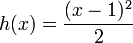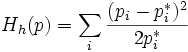это квадратичное приближение для (минус) энтропии Кульбака вблизи точки равновесия. С точностью до постоянного во времени слагаемого эта функция совпадает с (минус) энтропией Фишера, которую даёт следующий выбор,
, 
;
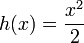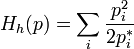это (минус) энтропия Фишера.
, 
;
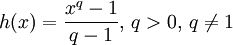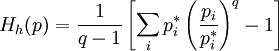это один из аналогов свободной энергии для энтропии Тсаллиса. Энтропия Тсаллиса (Tsallis entropy)
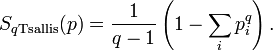
служит основой для статистической физики неэкстенсивных величин. При 
она стремится к классической энтропии Больцмана — Гиббса — Шеннона, а соответствующая функция Моримото — к (минус) энтропии Кульбака.
