2014-02-02
1472
Þ Пусть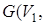 
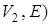- двудольный граф, в котором существует цикл С2п+ 1 нечетной длины. Пусть С2п+ 1 = v 1 – v 2 – … – v 2 n – v 2 n+ 1 – v 1. Положим для определенности, что 
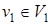. Тогда 
, …, 
, 
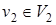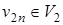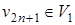, ребро (v 1, v 2 n+ 1) соединяет вершины из одной доли – противоречие.
Ü Пусть все простые циклы графа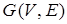 
имеют четную длину. Граф
Рис. 14
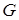будем считать связным, иначе каждую компоненту связности можно рассматривать отдельно. Разобьем вершины множества V на два непересекающихся подмножества V 1 и V 2 так.
1. Включим во множество V 1 произвольную вершину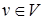 
.
2. Выделим ярусы вершины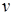
: D (v, 0), D (v, 1), D (v, 2), …. Вершины ярусов D (v, 2 k +1), k = 0, 1, 2, … включим во множество V 2. Вершины ярусов D (v, 2 k), k = 1, 2, … включим во множество V 1.
Тогда V 1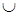 
V 2 = V; V 1 
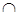V 2 = Æ.
Предположим, что в графе 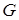есть вершины u и w, принадлежащие одной доле и соединенные ребром. Пусть для определенности u, w 
; 
.
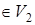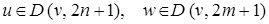Рассмотрим геодезические, соединяющие вершину v с вершинами u и w. Обозначим их < v, u > и < v, w >, а их длины обозначим |< v, u >| и |< v, w >|. В силу сказанного |< v, u >| = 2 п + 1, |< v, w >| = 2 m + 1.
|
|
|
Эти геодезические имеют общие вершины, например, v. Пусть v ¢ - наиболее удаленная от вершины v общая вершина геодезических (рис. 15). Может оказаться, что v ¢ = v.
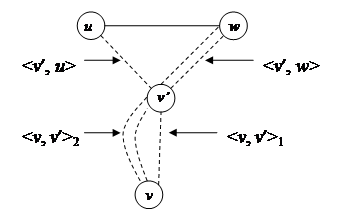
Рис. 15
Так как < v, v ¢>1 и < v, v ¢>2 – это участки геодезических, то и < v, v ¢>1 и < v, v ¢>2 – это геодезические, соединяющие вершины v и v ¢. Значит, они имеют одинаковую длину, |< v, v ¢>1| = | < v, v ¢>2 | = k.
Тогда длина простого цикла u – w – < w, v ¢ > – < v ¢, u > равна
1 + (2 n + 1 – k) + (2 m + 1 – k) = 1+2 m + 2 n + 2 – 2 k – нечетное число – противоречие.
