Производная и дифференциал.
Пусть функция 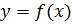 определена на некотором интервале
определена на некотором интервале  и
и 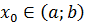 .
.
Производной функции 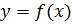 в точке
в точке 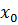 называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю, т. е.
называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю, т. е.

 .
.
Геометрический смысл производной.
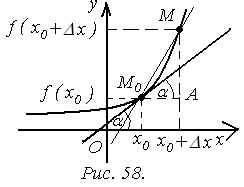 Пусть задана функция
Пусть задана функция 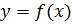 , непрерывная в некоторой окрестности точки
, непрерывная в некоторой окрестности точки 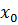 (рис. 58). Построим на осях координат точки
(рис. 58). Построим на осях координат точки 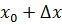 и
и 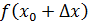 . Тогда длина
. Тогда длина 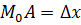 ,
, 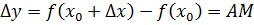 ,
, 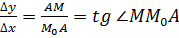 . При
. При 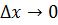 точка
точка 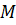 стремится к точке
стремится к точке 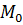 и в пределе совпадает с ней. Угол
и в пределе совпадает с ней. Угол 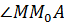 стремится к углу наклона касательной
стремится к углу наклона касательной 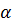 и в пределе совпадает с ним. Секущая
и в пределе совпадает с ним. Секущая 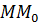 превращается в касательную к графику функции
превращается в касательную к графику функции  в точке
в точке 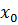 . Таким образом,
. Таким образом,
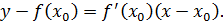
Пример 44. Написать уравнение касательной к графику функции  в точке
в точке 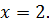
Решение. Так как 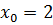 , то вычислим значения
, то вычислим значения 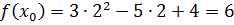 ,
, 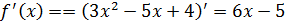 ,
,  . Окончательно получим
. Окончательно получим или
или 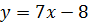 .
.
 2014-02-02
2014-02-02 200
200







