Пусть 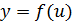 некоторая функция, где
некоторая функция, где 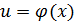 так же функция, тогда выражение
так же функция, тогда выражение  является функцией, которая называется сложной функцией от переменной
является функцией, которая называется сложной функцией от переменной 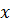 . Переменная
. Переменная 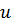 в этом случае называется промежуточной.
в этом случае называется промежуточной.
Теорема 25. Если функция 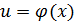 имеет производную
имеет производную 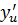 в точке
в точке 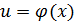 , то сложная функция
, то сложная функция  имеет производную
имеет производную 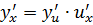 .
.
Доказательство. Пусть
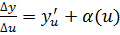 , или
, или 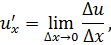
поэтому 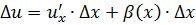 , где
, где 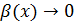 при
при 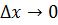 . Отсюда
. Отсюда 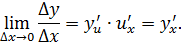
Рассмотрим примеры на применение теоремы 25.
Пример 48. Найти производную функции 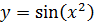 .
.
Решение. В нашем случае 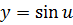 ,
, 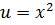 . По теореме 25 имеем
. По теореме 25 имеем
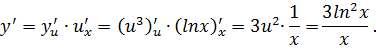
Пример 50. Найти производную функции 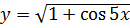 .
.
Решение. В нашем случае 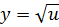 ,
, 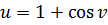 ,
, 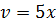 . По теореме 25 имеем
. По теореме 25 имеем
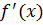 в произвольной точке этого интервала, то обратная ей функция
в произвольной точке этого интервала, то обратная ей функция 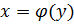 так же имеет производную
так же имеет производную 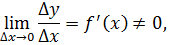
то имеем
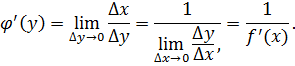
Пример 51. Рассмотрим функцию 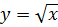 . Ее обратная
. Ее обратная 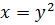 . Тогда по теореме 26
. Тогда по теореме 26
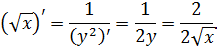
 2014-02-02
2014-02-02 286
286







