Определение. Говорят, что множество A содержится во множестве B (А – подмножество B, А включено в B, В содержит / включает A), если всякий элемент множества A принадлежит и множеству В. В этом случае пишут: 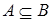 . Таким образом,
. Таким образом, 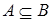 Û
Û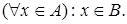
Можно сказать иначе: если 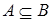 , то
, то 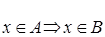 .
.
Одновременно верно и такое утверждение: если 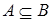 и
и 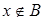 , то
, то 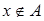 , ведь в противном случае
, ведь в противном случае 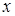 обязан принадлежать
обязан принадлежать 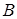 . Значит, можно записать: если
. Значит, можно записать: если 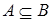 , то
, то 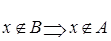 .
.
Определение. Говорят, что множество A есть собственноеподмножество множества B (В строго включает А) и пишут A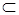 В, если
В, если 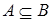 и В
и В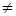 А.
А.
Таким образом, A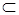 В Û
В Û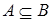 и
и 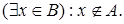
Определение. Если 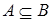 (A
(A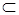 В), то множества А и В называются сравнимыми между собой.
В), то множества А и В называются сравнимыми между собой.
Ясно, что
· 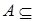 A для всякого множества A;
A для всякого множества A;
· Если 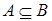 и
и 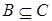 , то
, то 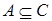 ; (
; (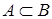 и
и  , то
, то 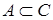 ).
).
Исходя из определения подмножества, опишем необходимые и достаточные условия того, что множество А не является подмножеством множества В (обозначение: А Ë В).
Именно, А Ë В Û 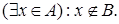 Во множестве А должен существовать хотя бы один элемент, не принадлежащий множеству В.
Во множестве А должен существовать хотя бы один элемент, не принадлежащий множеству В.
Утверждение. 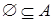 для всякого множества А.
для всякого множества А.
Доказательство. Пусть 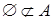 . Тогда
. Тогда 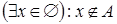 . Но данное условие противоречиво, пустое множество не содержит элементов.
. Но данное условие противоречиво, пустое множество не содержит элементов.
Пример. Пусть В = {1, {2}, {1}, {2, 3}, {1, 3}} и А 1 = {1, 2};
А 2 = {1, {1}}; А 3 = {2, 3}; А 4 = {{2, 3}}; А 5 = {1, {2, 3}, {1, 3}};
А 6 = {1, Æ}; А 7 = {{2}, {2, 3}, {1, 2, 3}}; А 8 = Æ.
Тогда А 1 Ë В (2 Ï В); А 2 Í В; А 3 Ë В (2 Ï В и 3 Ï В); А 4 Í В; А 5 Í В; А 6 Ë В (Æ Ï В); А 7 Ë В ({1, 2, 3} Ï В); А 8 Í В.
Определение. Булеаном множества А (обозначается 2 А) называется семейство всех подмножеств данного множества А.
Значит, 2 А= { B|B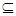 A }. В частности,
A }. В частности, 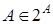 и
и 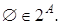
 2014-02-02
2014-02-02 673
673








