Примеры. Влияние электромагнитного поля на структуру и свойства металлических материалов

Влияние электромагнитного поля на структуру и свойства металлических материалов

Сверхпластичность

Под сверхпластичностью понимают способность металла к значительной равномерной деформации без деформационного упрочнения (наклепа).

Различают несколько видов сверхпластичности:

- мелкозеренная сверхпластичность проявляется при повышенных температурах, не ниже чем 0,4 Тпл, при очень мелком зерне размером в диаметре 3-5 мкм и малой скорости деформирования 0,0001 с^-1 (отсутствует сдвиговая деформация),

- субкритическая сверхпластичность. Имеет место при температурах вблизи или ниже фазовых превращений при определенной исходной структуре. Перед фазовым превращением или плавлением происходит значительное изменение свойств без изменения структуры. Например, Е снижается в два-три раза.

- мартенситная сверхпластичность, при сдвиговом бездиффузионном превращении наблюдается повышенная пластичность,

- рекристаллизационная сверхпластичность. Выше температуры рекристаллизации заметного упрочнения не возникает.

Влияние электромагнитного поля на структуру и свойства металлов в наибольшей степени проявляется в условиях протекания тока высокой плотности (до 100000000 А/м²) через очаг деформации. В данном случае возникает эффект электропластичности металлов, проявляющийся в значительном приращении деформации даже при комнатных температурах.

Протекание тока высокой плотности в металле вызывает увеличение плотности вакансий, длину пробега дислокаций, внутренний нагрев дефектных микрообъемов металла и повышение градиентов химических потенциалов.

Эффект электропластичности применяется в технологии волочения при изготовлении сверхтонких проволок и металлических волокон.

При электропластической обработке растут как прочностные, так и пластические характеристики.

1. Функция f(x) =(x -1)² является бесконечно малой при x →1, так как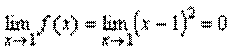

2. Функция f(x) = tg x – бесконечно малая при x →0.

3. f(x) = ln (1+ x)– бесконечно малая при x →0.

4. f(x) = 1/ x – бесконечно малая при x →∞.

Теорема 1. Если функция y=f(x) представима при x→a в виде суммы постоянного числа b и бесконечно малой величины α(x): f (x)=b+ α(x) то .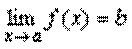

Обратно, если 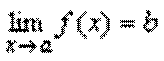, то f (x)=b+α(x), где a(x) – бесконечно малая при x→a.

Теорема 2. Алгебраическая сумма двух, трех и вообще любого конечного числа бесконечно малых есть функция бесконечно малая.

Теорема 3. Произведение бесконечно малой функции a(x) на ограниченную функцию f(x) при x→a (или при x→∞) есть бесконечно малая функция.

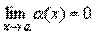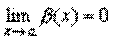Следствие 1. Если и , то .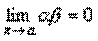

Следствие 2. Если 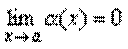и c= const, то .

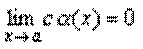Теорема 4. Отношение бесконечно малой функции α(x) на функцию f(x), предел которой отличен от нуля, есть бесконечно малая функция.

Функция f (x) называется бесконечно большой функцией в точке х = x ₀ (или x → x ₀), если для любого как угодно большого положительного числа K > 0 существует δ = δ(K) > 0, такое, что для всех х, удовлетворяющих условию 0 < | x – х ₀ | < δ, выполняется неравенство | f (x) | > К.
В этом случае пишут

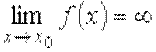
и говорят, что функция стремится к бесконечности при х → х ₀, или что она имеет бесконечный предел в точке х = х ₀. Если же в определении выполняется неравенство f (x) > K (f (x) < – K), то пишут

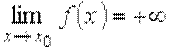или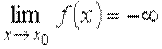

и говорят, что функция имеет в точке х ₀ бесконечный предел, равный + ∞ (– ∞).
По аналогии с конечными односторонними пределами определяются и бесконечные односторонние пределы:

, , , .

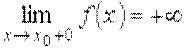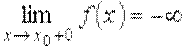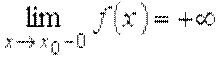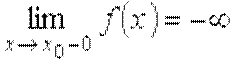Так, например, пишут 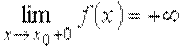если для любого как угодно большого положительного числа K > 0 существует δ = δ(K) > 0, такое, что для всех х, удовлетворяющих условию х ₀ < x < х ₀ + δ, выполняется неравенство f (x) > К. Или в символической записи

( K > 0) (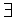 δ = δ(K)> 0)( x₀ < х < x₀+δ): f (x) > K.

Предлагается самостоятельно сформулировать определение бесконечно большой функции при x → + ∞, x → – ∞.