Наиболее распространенные ошибки

Основное внимание в программировании уделяется защите программ от неверных данных, но даже при правильных данных нет гарантии, что программа будет работоспособной. Рассмотрим алгоритм вычисления sin(x)=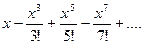

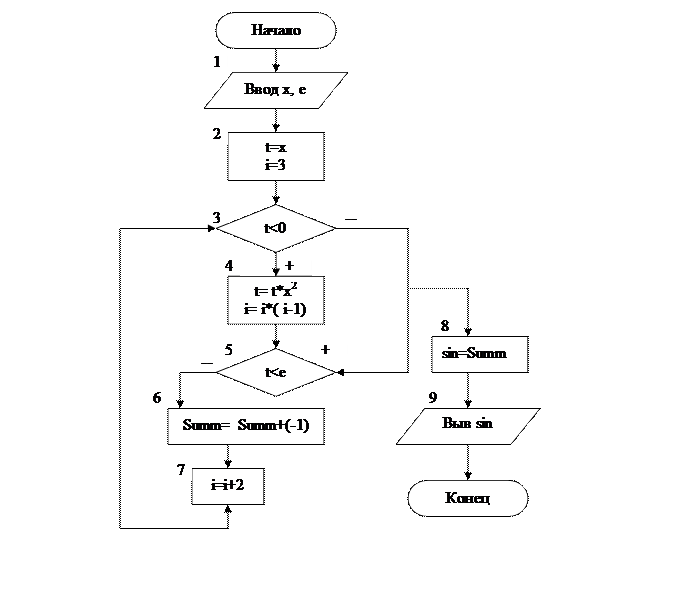
1. Из блок-схемы видно, что переменной Summ не было присвоено никакого значения. Поэтому в начальный момент значение этой переменной было произвольным и, как это происходит в большинстве систем, с каждым последующим обращением в ней накапливается еще больше «мусора».

Замечание. Перед использованием программы необходимо убедиться в том, что всем п6ременным присвоены начальные значения.

2. Предположим, что ввод х стандартное, тогда и t будет отрицательным, поэтому условие в блоке 5 будет истинным и будет иметь место немедленный выход из программы с выдачей неправильного результата, поэтому условие (5) нужно заменить на t<0/

3. В выражении (-1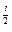), используемом для перемены знака, у членов ряда имеется ошибка и в такой записи его значение всегда будет (-1), поэтому для устранения ошибки надо использовать дополнительные скобки (-1) .

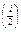Распространенным случаем ошибок являются ошибки типа «невпопад». К ним относятся, например, неправильное использование операций отношения, например, использование < вместо ≤, как требуется на самом деле.

Т.о., чтобы избежать наиболее распространенных ошибок, в программе необходимо:

1. присваивать начальные значения переменным перед тем, как они будут использоваться.

2. Быть внимательными к ошибкам типа «невпопад». Убедиться в том, что необходимые действия выполняются нужное число раз и что проверки на сравнение ветвятся правильно при достижении граничных значений.

3. Проверять, чтобы индексы при обращении к элементам массива не выходили за границы.

4. Избегать циклов с несколькими выходами из них. Для этого объединять проверки условий выхода из цикла и помещать их к его началу

5. Проверять могут ли циклы в программе при определенных обстоятельствах выполняться нулевое число раз.

6. Не использовать числа с плавающей «,» в качестве значений счетчиков (т.к. для дробных величин с плавающей запятой не всегда справедливы известные правила арифметики).