Экстремум функции. Пусть функция определена в окрестности точки x0

Пусть функция 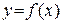определена в окрестности точки x₀.

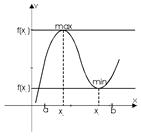
Определение: Точка x₀ называется точкой строгого локального максимума, если существует такая ее окрестность точки, в которой выполняется неравенство .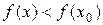

x₀ — max.

Определение: Точка x₀ называется точкой строгого локального минимума, если существует такая ее окрестность точки, в которой выполняется неравенство .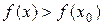

x₀ — min.

Точки локального максимума и минимума называются точками экстремума.

Необходимое условие экстремума дифференцируемой функции.

Если функция 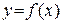, дифференцируемая в точке x₀, имеет в этой точке экстремум, то производная .

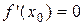Доказательство:

Пусть для определенности точка x₀ — max.

Тогда по определению существует такая ее окрестность 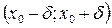, в которой выполняется неравенство < .

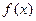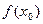Т.о. на интервале 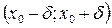в точке x₀ функция принимает наибольшее значение .

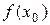Тогда по теореме Ферма: .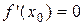

Аналогично доказывается для минимума функции.

Ч.т.д.

Однако, возможна ситуация, когда функция 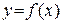будет иметь экстремум в точке x₀ в том случае, когда производная 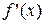не существует.

Точки, в которых производная 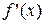либо равна 0, либо не существует, называются критическими точками производной.

Замечание 1: Обратное утверждение не верно. Не всякая функция, производная которой в точке равна нулю или не существует, имеет в этой точке экстремум.