Волгодонск
Конспект лекции №3
Висновок
На даній лабораторній я навчився опрацьовувати дані у Excel, сортувати та фільтрувати дані у списку, формувати підсумки. Навчився створювати зведені таблиці у EXCEL
по теме:
«Монотонность функции»
 |
Пусть функция 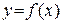 определена и непрерывна на промежутке (a;b).
определена и непрерывна на промежутке (a;b).
Определение: Функция 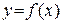 называется неубывающей (невозрастающей) на (a;b), если для любых x1<x2, принадлежащих (a;b), выполняется
называется неубывающей (невозрастающей) на (a;b), если для любых x1<x2, принадлежащих (a;b), выполняется 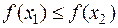 (
(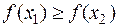 ).
).
Определение: Функция 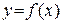 называется возрастающей (убывающей) на (a;b), если для любых x1<x2, принадлежащих (a;b), выполняется
называется возрастающей (убывающей) на (a;b), если для любых x1<x2, принадлежащих (a;b), выполняется  (
(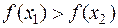 ).
).
Теорема 1.
Для того чтобы функция 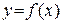 , дифференцируемая на (a;b), была возрастающей, необходимо, чтобы производная на этом промежутке была неотрицательна, т.е.
, дифференцируемая на (a;b), была возрастающей, необходимо, чтобы производная на этом промежутке была неотрицательна, т.е. 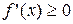 , и достаточно, чтобы
, и достаточно, чтобы 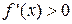 .
.
Доказательство:
Необходимость.
Пусть f(x) возрастает на (a;b). Тогда для любых 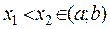 выполняется
выполняется  .
.
 Þ
Þ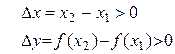 Þ
Þ 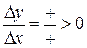 .
.
По определению производной: 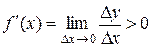 .
.
Достаточность.
Пусть 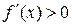 на (a;b). f(x) дифференцируема на (a;b). Выберем на этом промежутке 2 точки х1; х2.
на (a;b). f(x) дифференцируема на (a;b). Выберем на этом промежутке 2 точки х1; х2.
Тогда на (х1; х2) выполняется условие теоремы Лагранжа:
существует точка с Î(х1; х2) такая, что 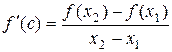 .
.
Þ 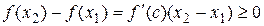 (т.к.
(т.к. 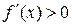 ).
).
Þ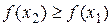 . Þ
. Þ 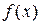 возрастает на (a;b).
возрастает на (a;b).
Ч.т.д.
Теорема 2.
Для того чтобы функция 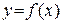 , дифференцируемая на (a;b), была убывающей, необходимо, чтобы производная на этом промежутке
, дифференцируемая на (a;b), была убывающей, необходимо, чтобы производная на этом промежутке 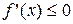 и достаточно, чтобы
и достаточно, чтобы 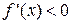 .
.
Доказательство проводится аналогично.
Пример: Найти интервалы возрастания и убывания функции 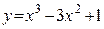 .
.
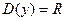 .
.

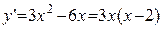 .
.
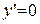 Þ
Þ 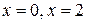 .
.
 2014-02-02
2014-02-02 3550
3550