2014-02-02
8366
В случае частного двух величин
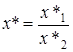
будем иметь:
,
.
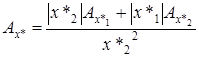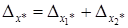Таким образом, относительные погрешности складываться при этом будут действовать те же правила, что и при умножении.
Задача 3. Вычислить значение функции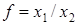 
. Найти абсолютную и относительную погрешности результата, считая все значащие цифры исходных данных верными, если 
, 
.
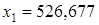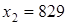Решение. Цифра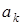 
считается верной, если 
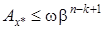или значащая цифра называется верной, если абсолютна погрешность числа не превышает ½ единицы разряда, который соответствует этой цифре. Тогда 
, 
.
.
.
.
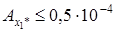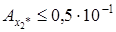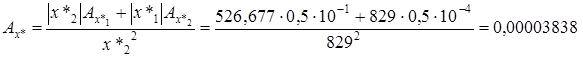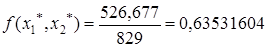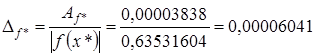Задача 4. Оценить погрешность функции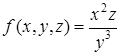 
, если x = 0,15±0,005, y = 2,13±0,01, z = 1,14±0,007.
Решение. По формуле для абсолютной погрешности результата имеем
.
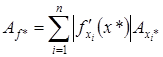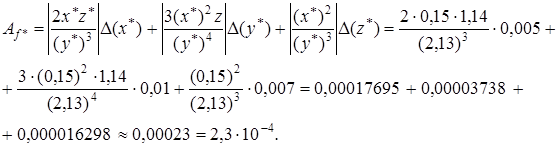
Найдем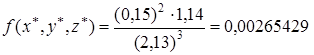 
.
.
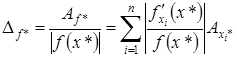Тогда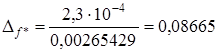 
.
Задача 5. Пусть числа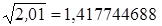
и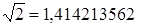 
заданы с десятью верными значащими цифрами. Сколько верных значащих цифр будет иметь число 
?
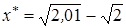Решение. Отнимая, получим x* = 0,003531126. Обозначим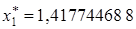 
, 
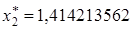. Тогда абсолютные погрешности 
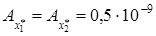. Абсолютная погрешность разности 
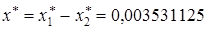будет равняться 
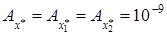. Цифра 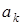считается верной, если 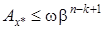. Из 10–9<0,5·10–8, то делаем вывод, что число x* имеет шесть верных значащих цифр 3,5,3,1,1,2.
