Погрешности округления

Рассмотрим простейшую гипотетическую ЭВМ в предположениях:

1. Все числа удовлетворяют условию .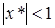

2. ЭВМ имеет запоминающее устройство, в котором можно хранить m разрядов.

3. ЭВМ может выполнять операции сложения, вычитания и умножения в накопителе 2m разрядов.

4. ЭВМ может выполнять операцию деления, причем первые m разрядов величины 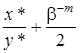помещаются в специальный счетчик, т.е. машина может округлять числа в накопителе путем прибавления к ним 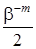и отбрасывания последних m разрядов.

Чтобы можно было произвести дей­ствия сложения и вычитания, нужно потребовать, чтобы были выполнены следующие условия:

, .

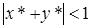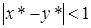Округлять при этом не придется, и следовательно, ошибок округления не возникает. Если нужно перемножить два каких-то числа, находящихся в каких-то ячейках запоминающего устройства, то модуль резуль­тата всегда будет меньше 1, а сам результат не может иметь более 2m разрядов. Таким образом, и в этом случае округлений не потре­буется. Но если этот результат придется выводить в какую-то ячейку запоминающего устройства или выводить из машины, то придется сделать округление. При этом мы уже не получим точ­ного произведения.

Обозначим результат округления произведения 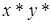как 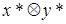, отличая его от точного произведения 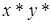. Будем называть 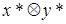псевдопроизведением. Аналогично обозначим результат округления деления 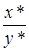как 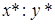, который будем называть псевдоделением. Тогда

,

.

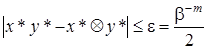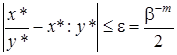Пусть теперь нужно образовать сумму произведений. При этом возможно получить сначала в специальном накопителе точную сумму произведений, а потом произвести округление. Такую псевдооперацию будем обозначать 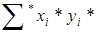. Таким образом,

.

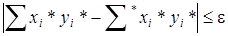При этом не все свойства обычных арифметических операций сохранятся для псевдоопераций. Так, например, дистрибутивный закон. Выражение 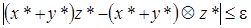, а 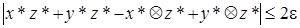, так как в первом случае производится одно псевдоумножение, а во втором два. Таким образом,

.

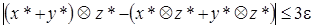Числа, разность которых стоит под знаком модуля, могут отли­чаться друг от друга на величину, кратную 2e, т.е. кратную еди­нице последнего разряда. Поэтому

.

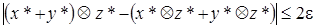Рассмотрим пример. Предположим, что 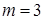, и нам нужно найти

(0,364 + 0,423)∙0,125

При этом

,

.

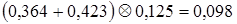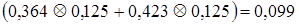Мы как раз получили разницу в единицу последнего знака.

Порядок, в котором производятся операции умножения и деле­нии, также будет иметь значение.

Пусть нам требуется найти вели­чину 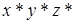. При этом

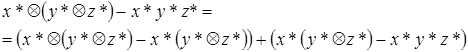
и, следовательно,

.

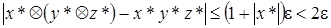Аналогично получим:

.

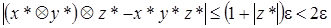Отсюда

.

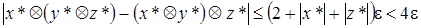Проводя те же рассуждения, что и в предыдущем случае, найдем:

.

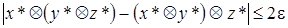Рассмотрим пример. Предположим, что 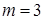, и нам нужно найти 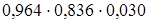. При этом

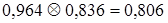и .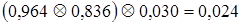

В то же время

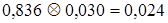и .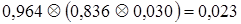

Пусть необходимо вычислить выражение 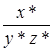. Будем предполагать, что 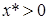, , 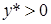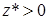и все операции можно произвести на нашей ЭВМ.

При вычислении этого вы­ражения в различной последовательности получим разные результаты.

Вычислим сначала 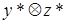и затем найдем 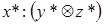. При этом

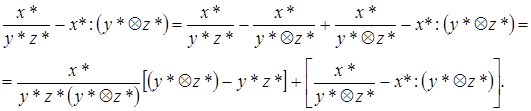
Второй член правой части оценивается без труда:

.

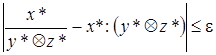Оценим первый член, предполагая, что 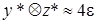, т.е. мало. Для того чтобы было возможно произвести деление, потребуем, чтобы 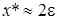. Так как

,

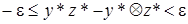то 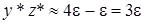или 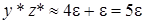. В первом случае оцениваемый член будет близок к

,

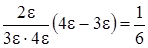во втором – к

.

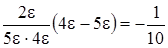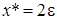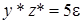Точное частное при и будет 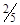и погрешность со­ставляет около 25%.

Так как для некоторых значений х*, у*, z* мы получили неудовлетворительный результат, то возьмем другую последовательность операций. Разделим сначала х* на у* и результат поделим на z*. Оценим

.

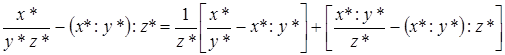Рассмотрим только первый член. Результат будет зависеть от того, что больше: у* или z*. Лучший результат получится при 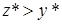. Рассмотрим этот случай. Так как 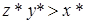(иначе деление невозможно было бы выполнить на машине), то 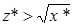. Т.к. 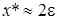, то 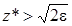. Отсюда

.

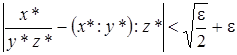Полученный результат лучше, чем предыдущий. Если 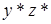немало, то первый способ вычислений может оказаться лучше второго.