Аналитически случайные погрешности измерений описывают с помощи математического аппарата теории вероятности и математической статистики. Наиболее общей характеристикой случайной величины является закон (функция) ее распределения.
В математике известны две формы описания закона: дифференциальная и интегральная.
Дифференциальным законом распределения случайной погрешности 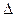 или плотностью распределения вероятностей (плотностью вероятностей) случайной погрешности
или плотностью распределения вероятностей (плотностью вероятностей) случайной погрешности 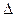 называется функция
называется функция 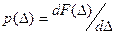 , где
, где 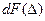 - вероятность нахождения погрешности Δ в интервале
- вероятность нахождения погрешности Δ в интервале 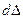 . В данном случае закон
. В данном случае закон 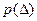 является одномерным.
является одномерным.
Интегральным законом распределения случайной погрешности Δ называется функция 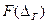 , выражающая вероятность Р того, что случайная погрешность находится в интервале от
, выражающая вероятность Р того, что случайная погрешность находится в интервале от 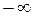 до некоторого значения, меньшего граничного
до некоторого значения, меньшего граничного 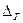 :
:

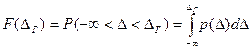
Функция 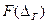 неубывающая и определена так, что
неубывающая и определена так, что 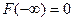 и
и 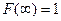 .
.
Практический интерес вызывает нахождение вероятности Р, с которой погрешность измерений Δ находится в некотором заданном интервале погрешностей (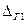 ,
, 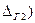 , где
, где
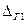 и
и 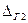 - нижняя и верхняя границы этого интервала.
- нижняя и верхняя границы этого интервала.
Записывается эта вероятность как 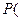
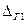 < Δ <
< Δ < 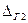 ) и в общем случае
) и в общем случае 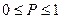 .
.
Для определения вероятности 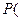
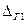 < Δ <
< Δ < 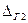 ) можно использовать и интегральный и дифференциальный законы распределения погрешностей Δ:
) можно использовать и интегральный и дифференциальный законы распределения погрешностей Δ:
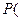
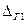 < Δ <
< Δ < 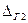 ) =
) = 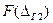 -
- 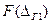
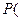
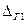 < Δ <
< Δ < 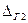 ) =
) = 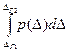 .
.
В метрологии чаще используется дифференциальный закон, так как он описывает свойства случайных погрешностей с большей наглядностью.
Из физических представлений следует, что вероятность нахождения погрешности Δ на интервале всех возможных значений погрешностей измерений, т.е в общем случае на интервале (- ∞, ∞) 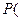
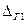 < Δ <
< Δ < 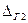 ) =
) = 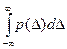 = 1.
= 1.
Это выражение в математике называется условием нормирования плотности распределения вероятностей р( Δ ). Оно означает, что площадь под графиком любой функции р( Δ ) на интервале всех ее значений должна быть равна 1.
Законы распределения случайных погрешностей могут быть симметричными или асимметричными относительно центра распределения погрешностей. В практической метрологии рассматриваются симметричные законы как наиболее распространенные.
Описание случайных погрешностей в виде законов распределения является наиболее полным, но экспериментальное определение этих законов требует весьма больших затрат времени. Однако во многих практических случаях нет необходимости описывать случайную погрешность полностью, достаточно охарактеризовать ее отдельные свойства. Такие числовые характеристики называются моментами.
Наиболее часто рассматривается центральный момент второго порядка, называемый дисперсией D = 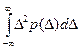 .
.
Дисперсия характеризует рассеяние погрешностей относительно центра распределения Δ=0.
Так как D имеет размерность квадрата погрешности, то обычно используют среднее квадратическое отклонение (СКО) 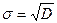 , которое имеет размерность погрешности.
, которое имеет размерность погрешности.
В практике измерений используется множество законов распределения, но наиболее часто используются нормальный (Гаусса), равномерный, трапецеидальный, треугольный (Симпсона), Стьюдента и др. законы.
Нормальный закон распределения погрешностей применяется в следующих предположениях:
¾ Погрешность может принимать непрерывный ряд значений в интервале ±∞;
¾ При выполнении значительного числа наблюдений большие погрешности Δ появляются реже, чем малые, а частота появления погрешностей, идентичных по величине и противоположных по знаку, одинакова.
Для нормального закона распределения:
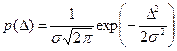
где 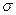 - среднеквадратичное отклонение погрешности ∆ характеризует точность выполненных измерений. Чем
- среднеквадратичное отклонение погрешности ∆ характеризует точность выполненных измерений. Чем 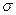 меньше, тем выше точность измерений. По мере уменьшения СКО
меньше, тем выше точность измерений. По мере уменьшения СКО 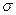 рассеяние случайных погрешностей ∆ относительно центра их распределения уменьшается.
рассеяние случайных погрешностей ∆ относительно центра их распределения уменьшается.
При нормальном законе формула для расчета вероятности 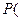
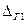 < Δ <
< Δ < 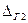 ) находится подстановкой
) находится подстановкой 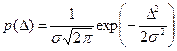 в
в 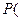
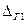 < Δ <
< Δ < 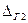 ) =
) = 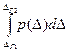 .
.
Для симметричного интервала (- 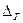 ,
, 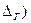 :
:
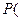 -
- 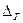 < Δ <
< Δ < 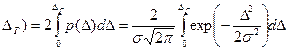 )
)
Геометрической интерпретацией этой вероятности для конкретного СКО 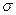 является величина площади фигуры, ограниченной функций
является величина площади фигуры, ограниченной функций 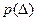 , отрезком оси ∆ от -
, отрезком оси ∆ от - 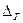 до
до 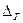 и ординатами
и ординатами 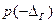 ,
, 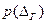 .
.
Чем шире заданный интервал погрешностей (- 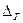 ,
, 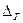 ), тем больше площадь S, т. е больше вероятность попадания случайных погрешностей в этот интервал. Для интервала погрешностей (-∞, ∞) вероятность
), тем больше площадь S, т. е больше вероятность попадания случайных погрешностей в этот интервал. Для интервала погрешностей (-∞, ∞) вероятность 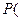 -∞< Δ <∞) = 1.
-∞< Δ <∞) = 1.
Для вычисления вероятности 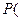
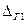 < Δ <
< Δ < 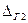 ) удобно в интеграле заменить переменную ∆ на
) удобно в интеграле заменить переменную ∆ на 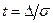 . При этом верхний предел заменяется на
. При этом верхний предел заменяется на 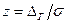 , а правая часть преобразуется в табулированный интеграл Ψ(z), который называется интегралом вероятностей:
, а правая часть преобразуется в табулированный интеграл Ψ(z), который называется интегралом вероятностей:
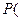 -z <t <z)=
-z <t <z)= 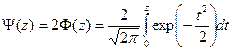
Функция 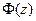 называется функцией Лапласа и выражает вероятность попадания случайной величины
называется функцией Лапласа и выражает вероятность попадания случайной величины 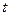 в интервал (0,z).
в интервал (0,z).
Задаваясь границей 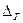 в долях
в долях 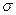 , находят
, находят 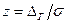 , а затем исходную вероятность по таблицам или графикам функции Ψ(z).
, а затем исходную вероятность по таблицам или графикам функции Ψ(z).
При необходимости можно осуществить обратные действия, т.е по заданной вероятности Ψ(z) найти z, далее 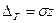 и интервал (-
и интервал (- 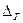 ,
, 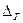 ).
).
Таблица и график интеграла вероятностей Ψ(z):
| z | Ψ(z) | z | Ψ(z) | z | Ψ(z) | z | Ψ(z) |
| 0,00 | 0,000 | 0,70 | 0,516 | 1,40 | 0,839 | 2,25 | 0,976 |
| 0,10 | 0,080 | 0,80 | 0,576 | 1,50 | 0,866 | 2,50 | 0,988 |
| 0,20 | 0,159 | 0,90 | 0,632 | 1,60 | 0,890 | 2,75 | 0,994 |
| 0,30 | 0,236 | 1,00 | 0,683 | 1,70 | 0,911 | 3,00 | 0,9973 |
| 0,40 | 0,311 | 1,10 | 0,729 | 1,80 | 0,928 | 3,30 | 0,9990 |
| 0,50 | 0,383 | 1,20 | 0,770 | 1,90 | 0,943 | 3,50 | 0.9995 |
| 0,60 | 0,452 | 1,30 | 0,806 | 2,00 | 0,955 | 4,00 | 0.9999 |
С помощью графика или таблицы можно найти значения вероятностей для некоторых, имеющих практическое значение интервалов погрешностей (- 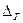 ,
, 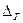 ), представленных в долях σ:
), представленных в долях σ:
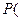 -
- 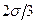 < Δ <
< Δ < 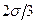 ) = 0,5;
) = 0,5;
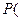 -
- 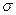 < Δ <
< Δ < 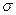 ) = 0,683;
) = 0,683;
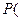 -3
-3 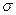 < Δ < 3
< Δ < 3 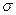 ) = 0,997;
) = 0,997;
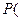 -∞< Δ <∞) = 1.
-∞< Δ <∞) = 1.
В соответствии со значениями этих вероятностей погрешность результатов измерений, равная 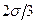 называется равновероятной (поскольку Р = 0,5).
называется равновероятной (поскольку Р = 0,5).
Погрешность, равная 3σ, принята в радиотехнике за максимальную, и записывается в виде М= 3σ. При Р =0,997 из тысячи выполненных измерений только три погрешности ∆ выходят за пределы интервала (-3 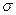 , 3
, 3 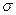 ).
).
Соответствующий интегралу вероятности закон распределения, представленный в зависимости от безразмерного аргумента 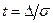 , называется нормированным нормальным законом и задается выражением:
, называется нормированным нормальным законом и задается выражением:
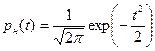 .
.
График нормированного нормального закона распределения 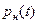 совпадает с графиком нормального закона, когда СКО σ = 1.
совпадает с графиком нормального закона, когда СКО σ = 1.
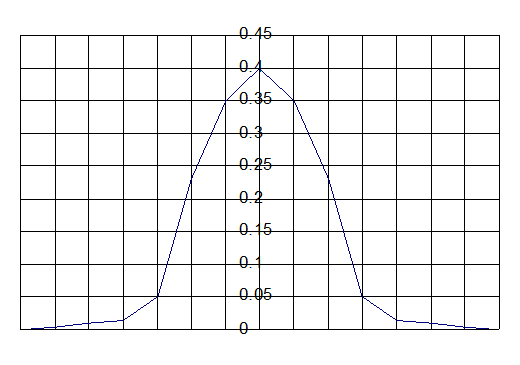
-7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7
Нормальный закон распределения случайных погрешностей широко используется при обработке результатов измерений, что объясняется следующими обстоятельствами. Случайная погрешность измерений некоторой величины складывается из многих составляющих, вызванных различными причинами, часто трудноуловимыми. Причем каждая из составляющих оказывает незначительное влияние на случайную погрешность. При этом такая случайная погрешность имеет закон распределения, близкий к нормальному. Для получения достаточно точных результатов обработки таких наблюдений их число n должно быть не менее 20.
При обработке небольшого числа (от 2 до 20) наблюдений физической величины, часто применяется закон распределения Стьюдента (псевдоним В.С. Госсета, предсказавшего это распределение), когда случайные погрешности распределены по нормальному закону.
Закон описывает распределение плотности вероятности значений случайной величины 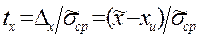 . Здесь
. Здесь 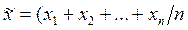 - оценка среднего арифметического ряда наблюдений 1 … n,
- оценка среднего арифметического ряда наблюдений 1 … n, 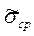 - оценка СКО случайной величины
- оценка СКО случайной величины 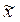 . Этот закон учитывает число выполненных наблюдений n и задается функцией:
. Этот закон учитывает число выполненных наблюдений n и задается функцией:
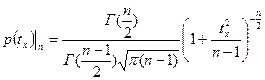
Здесь n≥2 - число наблюдени й; 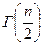 ,
, 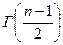 - гамма – функции (интегралы Эйлера), определяемые для некоторого аргумента х как
- гамма – функции (интегралы Эйлера), определяемые для некоторого аргумента х как 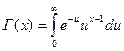 .
.
Отличия состоят в увеличении рассеяния относительных погрешностей относительно нуля по мере уменьшения числа наблюдений. При этом следует ожидать уменьшение вероятности Р попадания случайной величины 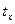 в заданный интервал (
в заданный интервал (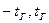 ).
).
Для поиска такой вероятности используется подстановка функции Стьюдента в общую формулу, заменив ∆ на относительную, а пределы интеграла 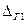 ,
, 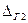 на равные ±
на равные ± 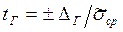 :
: 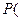 -
- 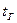 <
< 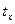 <
< 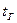 ) =
) = 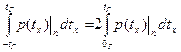
Отметим, что параметр 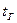 называется коэффициентом Стьюдента и для него принято специальное обозначение. В связи с тем, что при выполнении расчетов погрешностей измерений задаются некоторой доверительной вероятностью Р и числом наблюдений n, коэффициент Стьюдентаобозначают как
называется коэффициентом Стьюдента и для него принято специальное обозначение. В связи с тем, что при выполнении расчетов погрешностей измерений задаются некоторой доверительной вероятностью Р и числом наблюдений n, коэффициент Стьюдентаобозначают как 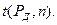 Значения коэффициента Стьюдента приведены в таблице:
Значения коэффициента Стьюдента приведены в таблице:
| n | 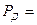 0,5 0,5 | 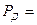 0,6 0,6 | 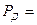 0,7 0,7 | 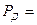 0,8 0,8 | 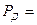 0,9 0,9 | 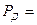 0,95 0,95 | 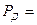 0,98 0,98 | 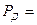 0,99 0,99 |
| 1.00 | 1.38 | 1.96 | 3.08 | 6.31 | 12.71 | 31.82 | 63.66 | |
| 0.82 | 1.06 | 1.34 | 1.89 | 2.92 | 4.30 | 6.97 | 9.93 | |
| 0.77 | 0.98 | 1.25 | 1.64 | 2.35 | 3.18 | 4.54 | 5.84 | |
| 0.74 | 0.94 | 1.19 | 1.53 | 2.13 | 2.78 | 3.75 | 4.60 | |
| 0.73 | 0.92 | 1.16 | 1.48 | 2.02 | 2.62 | 3.37 | 4.03 | |
| 0.72 | 0.91 | 1.13 | 1.44 | 1.94 | 2.45 | 3.14 | 3.71 | |
| 0.71 | 0.90 | 1.12 | 1.42 | 1.90 | 2.37 | 3.00 | 3.50 | |
| 0.71 | 0.89 | 1.11 | 1.40 | 1.86 | 2.31 | 2.90 | 3.36 | |
| 0.70 | 0.88 | 1.10 | 1.38 | 1.83 | 2.26 | 2.82 | 3.25 | |
| 0.69 | 0.87 | 1.07 | 1.34 | 1.75 | 2.13 | 2.60 | 2.95 | |
| 0.69 | 0.86 | 1.06 | 1.32 | 1.71 | 2.06 | 2.49 | 2.80 |
При использовании на практике коэффициентов Стьюдента задаются доверительной вероятностью 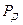 >0,9.
>0,9.
Равномерный закон распределения плотности вероятности характерен для поведения случайных погрешностей при измерении непрерывных физических величин методом дискретного счета (так называемые погрешности дискретизации) при преобразовании таких величин в аналогово-цифровых преобразователях (погрешности квантования уровней сигналов), а также для погрешностей отсчета показаний с различных шкал измерительных приборов.
Все возможные случайные погрешности результатов измерений, характеризуемых равномерным законом, расположены в некотором интервале 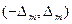 , где
, где 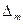 - максимальная погрешность. Аналитически плотность вероятности равномерного закона распределения погрешностей описывается соотношениями:
- максимальная погрешность. Аналитически плотность вероятности равномерного закона распределения погрешностей описывается соотношениями:
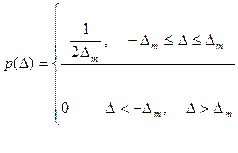
Вероятность того, что случайная погрешность результатов измерений ∆ находится в симметричном интервале 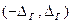 , определяется подстановкой в формулу интегрального закона значения плотности вероятности
, определяется подстановкой в формулу интегрального закона значения плотности вероятности 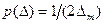 :
:
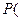 -
- 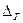 < Δ <
< Δ < 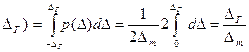 .
.
На графике плотности вероятности площадь прямоугольника с основанием 2 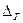 и высотой
и высотой 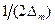 численно равна вероятности.
численно равна вероятности.
 P
P
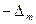
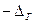 o
o 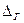
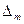
Для равномерного закона распределения погрешностей, симметричного относительно центра ∆ = 0, расчет СКО σ случайной погрешности выполняется по:
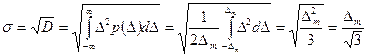
Треугольный закон распределения (закон Симпсона) характерен для случайных погрешностей цифровых измерительных приборов, в которых измеряемая величина преобразуется в пропорциональный интервал времени Тсч, называемый временем счета..
Измерение этого интервала выполняется с помощью счетных импульсов стабильного генератора, имеющих заданный период следования Т0. В связи со случайным положением счетных импульсов относительно интервала Тсч, а также случайным соотношением между периодом Т0 и временем счета Тсч треугольный закон представляет собой композицию (соединение) двух равномерных законов с одинаковыми максимальными погрешностями 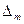 .
.
Для треугольного закона функция распределение плотности вероятности случайных погрешностей задается соотношением:
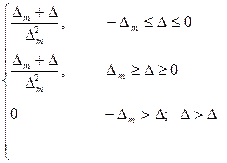
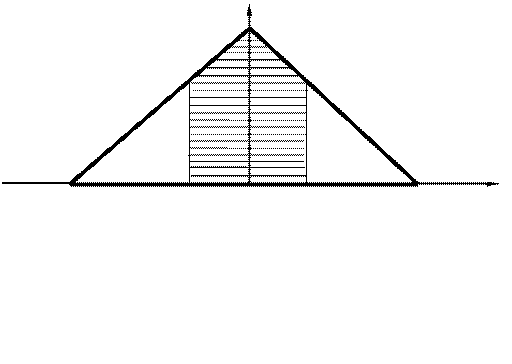
График треугольного закона распределения случайных погрешностей приведен ниже.
р
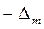
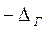 0
0 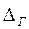
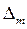
Заштрихованная область численно равна вероятности СКО σ.
Математическое выражение для этого закона вероятности того, что погрешность измерения ∆ располагается в интервале 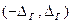 и выглядит:
и выглядит:
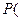 -
- 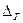 < Δ <
< Δ < 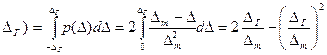
Как и в предыдущем случае, путем несложных вычислений получаем 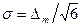 .
.
В практике радиоизмерений встречаются и другие законы распределения погрешностей (например, трапецеидальный, арксинуса и др.).
Если закон распределения неизвестен, то обычно принимают равномерное распределение погрешностей.
 2015-06-14
2015-06-14 4887
4887
