Решение задачи коммивояжера

Задача коммивояжера (см. разд. 4.3) является классическим примером задачи комбинаторной оптимизации, которая может быть решена методом ветвей и границ. Алгоритм решения, рассмотренный ниже, предложен Дж. Литлом, К. Мурти, Д. Суини и К. Кэрол в 1963 г.

Опишем процедуру ветвления BR, применяемую в этом алгоритме. Пусть полный взвешенный ориентированный граф 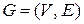с весовой функцией 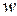моделирует города (множество вершин V) и расстояния между ними (взвешенные дуги E) в задаче коммивояжера. Тогда решение этой задачи сводится к отысканию кольцевого маршрута 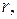проходящего через все вершины графа и имеющего минимальную сумму весов дуг, составляющих кольцевой маршрут (кратчайший кольцевой маршрут).

Пусть 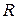– множество всех кольцевых маршрутов, проходящих через все вершины (без повторений) графа. Очевидно, что множество 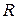соответствует множеству всех допустимых решений задачи коммивояжера.

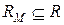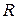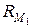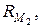
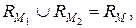
Процедура BR применяетсяк любому подмножеству (включая и само множество ) и разбивает его на два подмножества и 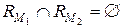одинаковой мощности 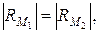где 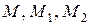– специальные метки подмножеств, принцип записи которых станет ясным позже.

Пусть 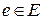– дуга графа 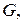имеющая начальную вершину 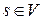и конечную вершину 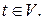Рассмотрим 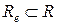– подмножество всех кольцевых маршрутов, включающих дугу 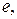и 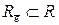– подмножество всех кольцевых маршрутов, не включающих дугу 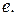Очевидно, что 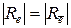, 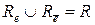и 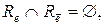т. е. предложенная процедура – это процедура разбиения множества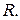

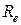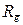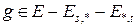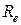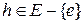Можно продолжить разбиение подмножеств и по тому же принципу. 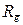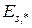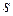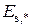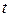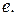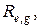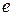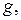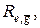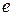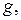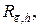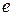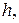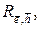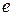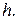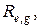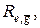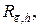Для этого выберем дуги: для разбиения и для разбиения , где – множество дуг, выходящих из начальной вершины , а – множество дуг, входящих в конечную вершину дуги Построим следующие подмножества кольцевых маршрутов: включающих дуги и включающих дугу и одновременно не включающих дугу не включающих дугу и одновременно включающих дугу не включающих дуги и Очевидно, что подмножества 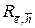являются равномощными, попарно не пересекаются, а их объединением будет множество 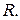Схематично принцип работы процедуры ветвления BR изображен на рис. 8.1.

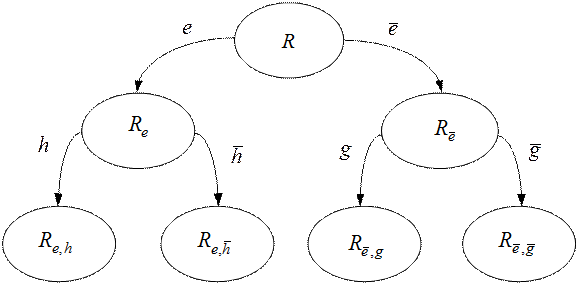
Рис. 8.1. Построение разбиений множества допустимых решений при решении задачи коммивояжера

Процедура EV вычисления нижней границы основывается на двух утверждениях, которые в силу их очевидности приводятся без доказательства.

Утверждение 1. Пусть 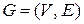– полный взвешенный граф с весовой функцие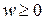й и 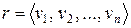– кратчайший кольцевой маршрут, проходящий через все вершины этого графа. Пусть далее 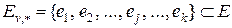– множество дуг, выходящих из вершины 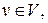а 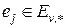– дуга, вес 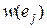которой не превышает веса всех остальных дуг из множества 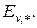Тогда, если веса всех дуг 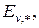выходящих из вершины 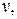уменьшить на величину 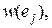то кратчайший маршрут останется прежним, но его вес снизится на величину

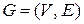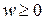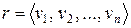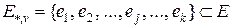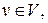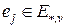Утверждение 2. Пусть – полный взвешенный граф с весовой функцией и – кратчайший кольцевой маршрут (последовательность вершин), проходящий через все вершины этого графа. Пусть далее – множество дуг, входящих в вершину а – дуга, вес 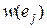которой не превышает веса всех остальных дуг из множества 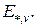Тогда, если веса всех дуг 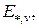входящих в вершину 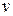уменьшить на величину 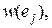то кратчайший маршрут останется прежним, но его вес снизится на величину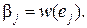

Таким образом, если последовательно для каждой вершины 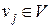графа 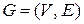вычислить значения 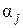и 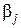, то величина 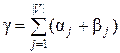будет составляющей веса кратчайшего кольцевого маршрута, но никогда его не превысит. Другими словами, 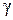можно использовать как нижнюю границу веса кратчайшего кольцевого маршрута.