2014-02-02
438
В замкнутых импульсных системах в отличие от непрерывных систем могут наблюдаться процессы, длительность которых конечна. Рассмотрим это на примере, когда входное воздействие имеет вид единичного скачка.
.
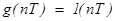Из (3.4) находим реакцию системы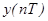 
на единичный скачок
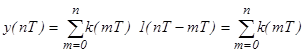
в силу того, что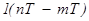 
= 1 при 
.
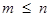Предположим, что
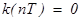при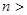 
l. (3.17)
Тогда
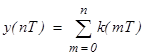при 
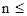l
и
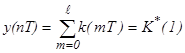= const при 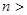l.
Условие 
записано исходя из того, что сумма ординат импульсной характеристики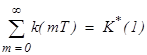 
. В рассматриваемом случае 
, т.к. при 
l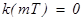 
.
Таким образом, при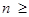 
l выходная координата остается постоянной величиной. Переходный процесс, вызванный единичным воздействием закончился за l тактов.
Итак
для осуществления процесса конечной длительности импульсная
характеристика замкнутой системы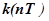 
начиная с некоторого момента
времени должна быть тождественно равной нулю: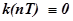 
, 
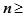l.
Рассмотрим требования, которые предъявляются к передаточным функциям замкнутых систем для реализации процессов конечной длительности.
Так как передаточная функция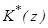 
с импульсной характеристикой 
связана соотношением
,
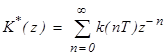то при выполнении условия (3.17)
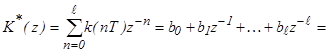
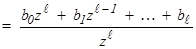. (3.18)
Из последнего уравнения видно, что для реализации процессов конечной длительности необходимо, чтобы полюсы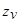 
передаточной функции замкнутой импульсной системы 
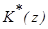находились в начале координат плоскости z, т.е. 
, 
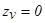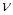=1, 2, …, l…
