Условие грубости

На первый взгляд может показаться, что обеспечив условие реализуемости, т.е. обеспечив требуемую разность порядков передаточной функции 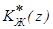можно добиться любого желаемого качества работы замкнутой системы. Например, если разность порядков знаменателя и числителя равна единице, а это условие практически выполняется всегда, то можно выбрать в качестве желаемой передаточной функции системы

=,

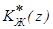добившись, на первый взгляд, того, что будет реализован процесс конечной длительности. В системе выходная координата через один такт принимает заданное значение (предполагается, что управляющее воздействие постоянное) вне зависимости от порядка 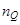неизменяемой части системы с передаточной функцией .

Однако при 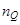³2 добиться желаемой передаточной функции в замкнутой системе можно, если полюса и нули неизменяемой части сократятся с нулями и полюсами цифрового регулятора.

Используемые при проектировании передаточные функции никогда точно не описывают динамику неизменяемой части (объекта). Поэтому нули и полюса сокращаются не точно, а только приближенно. Что касается нулей и полюсов , которые расположены на плоскости z внутри круга единичного радиуса, то неточность их сокращения, как правило, приводит к незначительным отклонениям характеристик замкнутой системы от желаемых. Если же полюсы или нули располагаются на и вне круга единичного радиуса (по модулю они равны или превосходят единицу), то при сколь угодно малой неточности в реализации цифрового регулятора или при сколь угодно малом изменении параметров неизменяемой части замкнутая система становится неустойчивой, что свидетельствует о ее не грубости.

Таким образом

условие грубости требует, чтобы передаточная функция цифрового регулятора 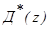не содержала нулей и полюсов, близких к нулям и полюсам передаточной функции неизменяемой части системы , располагающихся на и вне круга единичного радиуса.

Для выполнения условия грубости необходимо, чтобы желаемая передаточная функция замкнутой системы 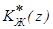(см. уравнение (8.4)) содержала нули , т.е. нули , расположенные на и вне окружности единичного радиуса, а 1– 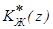содержала все нули 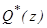, т.е. все полюсы , расположенные на и вне окружности единичного радиуса.

Если непрерывная часть системы устойчива, то и приведенная непрерывная часть системы с передаточной функцией будет устойчивой, а все полюсы этой функции будут располагаться внутри круга единичного радиуса. Что же касается нулей, то даже в случае, когда непрерывная часть системы минимально-фазовая, они могут быть расположены как внутри, так и вне круга единичного радиуса.