ЛЕКЦИЯ 3
Плоскопараллельное движение твёрдого тела
Вопросы лекции.
1. Общие понятия и закон плоскопараллельного движения тела.
2. Определение скорости и ускорения произвольной точки тела.
3. Мгновенный центр скоростей (МЦС) и его определение. Определение скоростей точек тела с помощью МЦС.
Тарг, 2009, с. 127 – 145.
 Движение твёрдого тела, при котором все его точки движутся в плоскостях, параллельных некоторой неподвижной плоскости, называется плоскопараллельным движением тела.
Движение твёрдого тела, при котором все его точки движутся в плоскостях, параллельных некоторой неподвижной плоскости, называется плоскопараллельным движением тела.
Неподвижная плоскость, о которой идёт речь в определении, называется основной, или опорной.
Рассмотрим тело, совершающее плоскопараллельное движение. Пусть P – опорная плоскость. Между точками тела проведём отрезок АВ  .
.
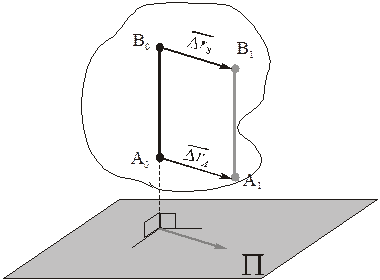
Легко доказать, что любой такой отрезок движется поступательно. Действительно, точки А и В движутся в параллельных плоскостях,  отрезки А0А1 и В0В1 либо параллельны, либо являются скрещивающимися. Но так как
отрезки А0А1 и В0В1 либо параллельны, либо являются скрещивающимися. Но так как 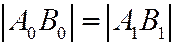 , то указанные отрезки могут быть только параллельными.
, то указанные отрезки могут быть только параллельными. 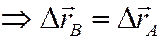 ,
,  все точки таких отрезков движутся одинаково.
все точки таких отрезков движутся одинаково.
Отсюда вытекает, что все сечения тела, параллельные опорной плоскости, движутся одинаково
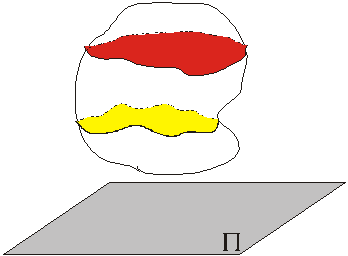
и можно перейти к изучению движения плоской фигуры (сечения тела), движущейся в своей плоскости.
Геометрия движения плоской фигуры в своей плоскости определяется двумя теоремами о перемещениях плоской фигуры.
Теорема 1. Любое перемещение плоской фигуры можно произвести, перемещая её поступательно вместе с какой-либо точкой, называемой полюсом, и поворачивая фигуру вокруг полюса.
Следствие. Поступательная часть перемещения зависит от выбора полюса, а вращательная часть – не зависит.
Теорема 2. Любое непоступательное перемещение плоской фигуры можно произвести одним поворотом вокруг некоторой точки, называемой центром конечного поворота.
Из приведенных теорем следует, что для задания плоскопараллельного движения надо задавать поступательную и вращательную составляющие движения плоской фигуры.
С началом в полюсе строим две системы координат: систему, которая движется поступательно относительно основной Oxyz; систему Ax1y1z1, связанную жестко с плоской фигурой.
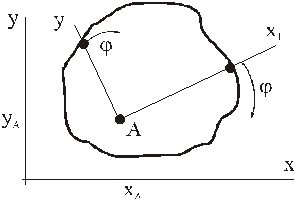
Задавая координаты xA, yA точки А как функции от времени, зададим поступательную часть движения фигуры, а, задавая угол j – вращательную часть движения фигуры.
Следовательно, тройка функций
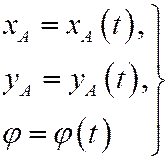
представляет закон (или уравнения) плоскопараллельного движения тела (плоской фигуры).
Зная функции (1) можно получить уравнения движения любой точки плоской фигуры. Например, если положение точки задано координатами x1, y1, то можно получить


согласно формулам перехода от одной системы координат к другой.
 2014-02-02
2014-02-02 3246
3246