2014-02-02
667
К средним показателям ряда динамики относятся
- средний уровень ряда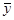 
;
- средний абсолютный прирост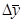 
;
- средний темп роста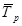 
;
- средний темп прироста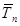 
.
Средний абсолютный прирост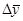 
рассчитывается только по цепному методу. Он характеризует, на сколько увеличился или уменьшился уровень явления:
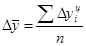, n – число цепных абсолютных приростов
Средний уровень ряда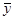 
в зависимости от целей социально-экономических исследований и исходных данных может определяться по двум формулам: средней арифметической взвешенной и средней хронологической.
Если дан интервальный динамический ряд с равными интервалами, то средний уровень определяется по формуле средней арифметической взвешенной:
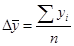, n – число уровней
Для интервальных рядов с неравными интервалами необходимо перейти к равным интервалам и определять средний уровень по формуле средней арифметической простой.
Для моментных рядов с равными интервалами средний уровень определяется по формуле средней хронологической:
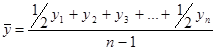
Для моментных рядов с неравными интервалами средний уровень определяется по формуле средней арифметической взвешенной:
|
|
|
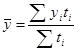
Средний темп роста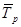 
показывает, во сколько в среднем выросло или уменьшилось явление; основан на расчете ценных показателей.
,
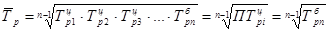где n-1 – число уровней «-»1;
n – число цепных .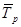
Средний темп прироста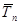 
:
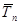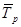=-100%
Если средний уровень ряда динамики снижается, то средний темп роста 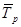<100%, а средний темп прироста 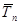<0. Отрицательное значение темпа прироста представляет собой теп сокращения и характеризует среднюю относительную скорость снижения уровня.
