Одной из важнейших задач статистики является определение в ряде динамики основной тенденции развития (тренда). Тренд – плавное и устойчивое изменение уровня явления во времени, свободное от случайных колебаний. Для выявления тренда применяются 3 основных метода:
1. метод укрупнения интервалов;
3. аналитическое выравнивание.
Метод укрупнения интервалов
Смысл метода заключается в том, что мы переходим от менее крупных интервалов к более крупным (от данных месяца к квартальным данным, от квартальных – к годовым и т.д.). Уровни новых укрупненных интервалов вычисляются путем суммирования уровней за периоды, вошедшие в новый интервал, или путем вычисления среднего уровня по укрупненному интервалу.
Пример: Динамика объема продаж телевизоров в 2002 году
| месяцы | |||||||||
| объем продаж в месяц | 2,0 | 2,2 | 2,1 | 3,0 | 2,9 | 2,6 | 2,6 | 3,2 | 2,9 |
| объем продаж в квартал | 6,3 | 8,5 | 8,7 | ||||||
| средний объем продаж | 2,1 | 2,7 | 2,9 |
Сущность метода заключается в том, что вычисляется средний уровень из определенного числа данных, обычно нечетного, в первых по счету уровнях ряда, затем из такого же числа уровней ряда, но начиная со второго по счету, далее начиная с третьего и т.д., т.е. средняя как бы скользит по динамическому ряду, передвигаясь на один срок.
Пример: Данные урожайности зерновых культур
| Год | Фактический уровень | Скользящая средняя | |
| Трехлетняя | Пятилетняя | ||
 15,4 15,4 | - | - | |
 14,0 14,0 | 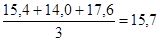 | - | |
 17,6 17,6 | 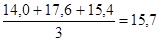 | 14,7 | |
| 15,4 | 14,6 | 15,1 | |
| 10,9 | 14,6 | 15,2 | |
| 17,5 | 14,15 | 17,1 | |
| 15,0 | 17,0 | 16,8 | |
| 18,5 | 15,9 | 17,6 | |
| 14,2 | 15,9 | - | |
| 14,9 | - | - |
Если применяется четная скользящая средняя (4-хлетняя, 6-тимесячная и т.д.), то после определения скользящей средней производят центрирование, т.е. полученные средние включают в интервал, состоящий из двух уровней, и находят среднюю в каждом интервале. Эти средние и будут окончательными центрированными средними.
Аналитическое выравнивание
Цель аналитического выравнивания – на основе полученного тренда получить обобщенную статистическую оценку закономерности развития социально-экономического явления, т.е. построить математическую модель, адекватно характеризующую социально-экономический процесс.
В основе метода лежит функция времени – теоретическая функция 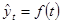 .
.
Определение теоретических уровней (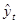 ) производится на основе адекватной математической модели, которая наилучшим образом отражает динамику вашего явления. Выбор типа модели зависит от цели исследования и от графического изображения тренда. Выбор математической функции можно осуществлять по показателям динамики:
) производится на основе адекватной математической модели, которая наилучшим образом отражает динамику вашего явления. Выбор типа модели зависит от цели исследования и от графического изображения тренда. Выбор математической функции можно осуществлять по показателям динамики:
1. Если развитие равномерное (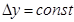 ), то явление описывается прямой:
), то явление описывается прямой:
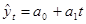
2. Если развитие равноускоренное или равнозамедленное, темп прироста 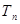
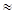 0, то уравнение описывается параболой второго порядка:
0, то уравнение описывается параболой второго порядка:

3. Если развитие уровней происходит с переменным ускорением или замедлением, темп прироста 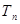 = var, то график будет иметь вид параболы третьего порядка:
= var, то график будет иметь вид параболы третьего порядка:

Пример аналитического выравнивания:
Допустим, явление развивается равномерно и описывается линейной функцией. Нужно рассчитать параметры уравнения 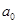 и
и 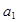 (коэффициенты регрессии).
(коэффициенты регрессии).
Расчет параметров функции обычно производится методом наименьших квадратов:
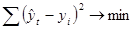
Этому условию будет удовлетворять следующая система двух линейных (нормальных) уравнений:
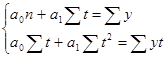 ,
,
где 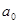 ,
, 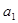 - искомые параметры уравнения;
- искомые параметры уравнения;
t – время (порядковый номер периода);
n – число уровней;
у – фактический уровень ряда.
Решается эта система при следующем условии:
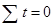
В этом случае центральный период (интервал или момент времени) =0.
Для четного ряда динамики:
| -5 | -3 | -1 | +1 | +3 | +5 |
Для нечетного ряда:
| -3 | -2 | -1 |
При подстановке 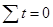 в исходную систему
в исходную систему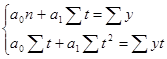 получаем:
получаем:
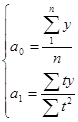
Полученные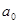 и
и 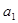 подставляем в уравнение
подставляем в уравнение 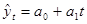 .
.
По полученному уравнению, подставляя вместо t исходные теоретические уровни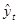 . По теоретическим уровням строим функцию или график функции
. По теоретическим уровням строим функцию или график функции 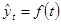 и визуально определяем совпадение или несовпадение наших кривых. Полученный график функции будет характеризовать временной тренд или основную тенденцию изучаемого явления. Правильность расчетов можно определить с помощью
и визуально определяем совпадение или несовпадение наших кривых. Полученный график функции будет характеризовать временной тренд или основную тенденцию изучаемого явления. Правильность расчетов можно определить с помощью
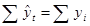 (расхождение не больше 2%)
(расхождение не больше 2%)
Для оценки адекватности выбранной математической модели (нескольких моделей) рассчитывают показатель адекватности математической модели, который называется стандартизированной ошибкой аппроксимации:
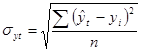
По величине этой ошибки судят об адекватности полученной математической модели. Если мы подобрали к тренду несколько моделей, то более адекватной будет та, у которой ошибка аппроксимации будет меньше.
 2014-02-02
2014-02-02 796
796







