1. Метод параллельных рядов – сопоставляют ряд значений факторного признака и соответствующие значения результативных признаков. Значения факторного признака располагают в порядке возрастания и затем прослеживают направление изменения результативного. Результативный признак – у, факторный – х.
Если 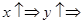 наличие прямой корреляционной связи.
наличие прямой корреляционной связи.
Если 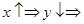 обратная связь.
обратная связь.
2. Построение корреляционной таблицы: х располагают в строках; у – в колонках. Числа, расположенные на пересечении строк и столбцов таблицы, показывают частоту повторения данного сочетания х и у.
Пример:
| 0,435 | 0,665 | 0,895 | 1,125 | 1,355 | fx | 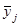 | ||||
| 0,32-0,55 | 0,55-0,78 | 0,78-1,01 | 1,01-1,24 | 1,24-1,47 | |||||||
| 0,22 0,24 0,26 0,30 0,32 | 1,01 1,079 0,895 0,780 0,435 | ||||||||||
| fy |
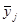 - среднее значение результативного признака для j -й группы значений факторного признака;
- среднее значение результативного признака для j -й группы значений факторного признака;
fx – частота повторений данного варианта х во всей совокупности;
fy - частота повторений данного варианта у во всей совокупности.
Если частоты в таблице расположены на диагонали из левого верхнего угла в правый нижний угол, т.е. большему значению х соответствует большее значение у, то имеет место прямая связь между признаками. Если частоты расположены на диагонали справа налево, то связь обратная.
Корреляционная таблица позволяет компактно изложить материал.
3. Построение групповой таблицы (аналитическая группировка).
Все наблюдения разбиваются на группы в зависимости от величины х и по каждой группе вычисляются средние значения у. Рост среднего значения у влечет за собой снижение х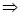 наличие обратной связи. При рассмотрении средних значений у корреляционная зависимость проявляется в большей степени, так как повышается влияние прочих факторов
наличие обратной связи. При рассмотрении средних значений у корреляционная зависимость проявляется в большей степени, так как повышается влияние прочих факторов 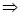 ясней зависимость между у и х, положенным в группировку.
ясней зависимость между у и х, положенным в группировку.
Пример:
| Группы партий деталей по уровню средней занятости рабочего места, ч. | Сумма значений результативного признака по группам, у | Число партий деталей в группе | Среднее значение результативного признака в группе, 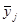 |
| 0,22 0,24 0,26 0,30 0,32 | 3,76 5,08 2,63 3,09 2,02 | 1,253 1,016 0,877 0,773 0,404 | |
| Итого: | 16,58 | 0,829 |
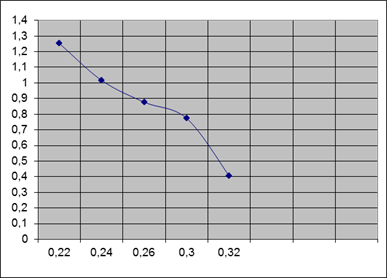
4. Графический метод: на основе значений у и х строится график (точечный) – поле корреляции.
Пример:
 | |||
| |||

|









|
9.2 Однофакторный корреляционный и регрессионный анализ. Показатели тесноты связи дают возможность охарактеризовать степень зависимости вариации результативного признак от вариации х.
Линейный коэффициент корреляции r (предложен Пирсоном)
При расчете этого показателя учитываются знаки отклонений индивидуальных значений признака от средней и сами величины таких отклонений, т.е.
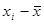 и
и 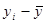 .
.
Для сравнения эти отклонения необходимо выразить в относительных величинах 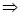 нормированные отклонения.
нормированные отклонения.
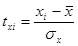 ;
; 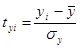
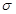 - среднее квадратическое отклонение.
- среднее квадратическое отклонение.
Среднее произведение нормированных отклонений есть линейный коэффициент корреляции r:
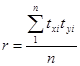
После преобразований получаем:
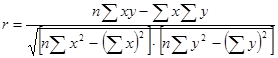
r изменяется от -1 до +1. Чем ближе r по абсолютной величине к 1, тем теснее связь между признаками. «+» - прямая зависимость; «-» - обратная.
r 2 – коэффициент детерминации.
r не является доказательством причинно-следственной связи между признаками, а является оценкой степени взаимной согласованности изменяющихся признаков.
Необходимо оценить существенность r – с помощью критериев в зависимости от объема выборочной совокупности. (В основе совокупности нормальное распределение.)
1) При большом объеме выборки:
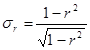 - средняя квадратическая ошибка коэффициента корреляции r.
- средняя квадратическая ошибка коэффициента корреляции r.
Если r > 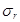 больше, чем в
больше, чем в 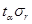 раз, то
раз, то 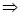 существенность r. (
существенность r. (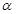 - уровень значимости: 0,01 или 0,05).
- уровень значимости: 0,01 или 0,05).
Если 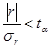 , то с вероятностью (1-
, то с вероятностью (1-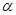 ) корреляционная связь отсутствует в генеральной совокупности.
) корреляционная связь отсутствует в генеральной совокупности.
2) Для малой выборки используется критерий Фишера. При этом 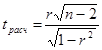 при r =0 распределена по закону Стьюдента с (n-2) степенями свободы.
при r =0 распределена по закону Стьюдента с (n-2) степенями свободы.
tрасч сравнивается с tтабл
Если tрасч> tтабл 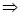 невероятно, что найденное значение r обусловлено только случайным совпадением х и у в выборке из генеральной совокупности, для которой r =0.
невероятно, что найденное значение r обусловлено только случайным совпадением х и у в выборке из генеральной совокупности, для которой r =0.
Если tрасч< tтабл 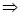 r =0 в генеральной совокупности
r =0 в генеральной совокупности 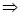 совпадение х и у случайно.
совпадение х и у случайно.
3) Проверка гипотезы по таблице Фишера без вычислений. Для числа степеней свободы (n-2) и уровней значимости 0,01 или 0,05 определяют rтабл. Сравнивают rрасч и rтабл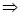 наличие связи между изучаемыми признаками в генеральной совокупности.
наличие связи между изучаемыми признаками в генеральной совокупности.
rрасч > rтабл 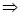 наличие связи
наличие связи
Эмпирическое корреляционное отношение 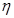
При наличии криволинейной зависимости между признаками используют эмпирическое корреляционное отношение 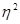 .
.
Расчет 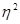 основан на теореме сложения дисперсий:
основан на теореме сложения дисперсий:
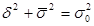
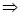
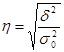 или
или 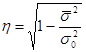 ,
,
где 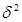 - межгрупповая дисперсия;
- межгрупповая дисперсия;
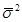 - средняя из внутригрупповых.
- средняя из внутригрупповых.
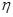 оценивает долю, которую составляет вариация результативного признака под давлением фактора х в общей вариации у.
оценивает долю, которую составляет вариация результативного признака под давлением фактора х в общей вариации у.
Если 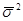
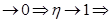 есть связь между х и у, т. е. вся вариация у обусловлена действием фактора х. Направление связи определяется по таблицам
есть связь между х и у, т. е. вся вариация у обусловлена действием фактора х. Направление связи определяется по таблицам
Вычисление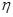 возможно при большом числе данных n, оформленных в виде таблиц. При малых n вносится поправка:
возможно при большом числе данных n, оформленных в виде таблиц. При малых n вносится поправка:
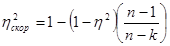
 2014-02-02
2014-02-02 1045
1045
