Уравнение регрессии. 1) Важным этапом регрессионного анализа является определение типа функции, с помощью которой характеризуется зависимость между признаками

1) Важным этапом регрессионного анализа является определение типа функции, с помощью которой характеризуется зависимость между признаками: 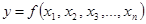. На основании теоретической функции строится теоретическая кривая (линия), вокруг которой группируются точки корреляционного поля и которая дает основное направление, основную тенденцию связи. Теоретическая линия изображает изменение средних величин результативного признака у при изменении х при полном взаимопогашении всех прочих, случайных по отношению к х факторов.

2) Теоретическая линия связи строится на основе эмпирических данных:

· эмпирической линии регрессии, которая является ломаной, так как имеется влияние неучтенных причин из-за недостаточности наблюдений;

· по опыту предыдущих исследований.

3) По эмпирической кривой выбирают приблизительный тип функции 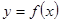. Наиболее часто для характеристики связей экономических явлений используют типы функций:

· линейная: ;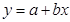

· показательная: ;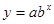

· степенная: .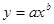

4) Для 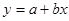необходимо определить коэффициенты a и b с помощью метода наименьших квадратов (сумма квадратов отклонений эмпирических точек от теоретической линии = min).

После преобразований получаем систему нормальных уравнений для линейной корреляционной связи:

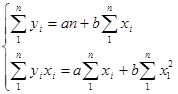
Если данные сгруппированы и имеется частота повторений f_x и f_y, то система уравнений имеет вид:

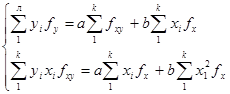
Решив эту систему уравнений, получаем a и b.

b – коэффициент регрессии, показывает, на сколько в среднем изменяется величина результативного признака у при изменении х на единицу. Геометрически b оценивает степень наклона прямой линии, изображающей уравнение .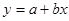

Необходимо оценить степень достоверности уравнения регрессии. Для этого используют среднюю квадратическую ошибку уравнения:

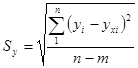где 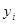- фактическое значение результативного признака;

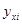- по уравнению регрессии;

m - число параметров (коэффициентов) в уравнении.

Чем меньше 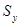, тем меньше рассеивание эмпирических точек вокруг прямой.

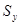указывает с определенной вероятностью, что величина результативного признака (у) окажется в определенном интервале относительно значения, вычисленного по уровню регрессии.