В любой момент времени (рис. 64) можно записать, что
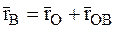
и, учитывая соотношение  получим:
получим:
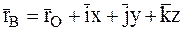 . (7.1)
. (7.1)
В этом выражении:
 – определяет положение МТ в ее абсолютном движении,
– определяет положение МТ в ее абсолютном движении,
x, y, z – определяют положение МТ в ее относительном движении,
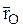 ,
,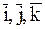 – определяют положение подвижной системы координат по отношению к неподвижной системе координат, т. е. переносное движение МТ.
– определяют положение подвижной системы координат по отношению к неподвижной системе координат, т. е. переносное движение МТ.
Возьмем производную по времени от выражения (7.1), учитывая, что единичные вектора 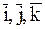 изменяются с течением времени по направлению:
изменяются с течением времени по направлению:
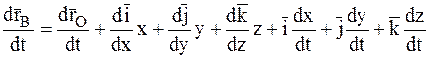 . (7.2)
. (7.2)
Так как 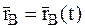 – уравнение абсолютного движения МТ, то в выражении (7.2):
– уравнение абсолютного движения МТ, то в выражении (7.2):
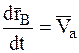 . (7.3)
. (7.3)
Так как x=x(t), y=y(t), z=z(t) – уравнения относительного движения МТ (производные от векторов 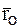 ,
,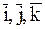 не входят в это выражение, т. е. подвижная система координат как бы условно считается неподвижной), то в выражении (7.2):
не входят в это выражение, т. е. подвижная система координат как бы условно считается неподвижной), то в выражении (7.2):
 . (7.4)
. (7.4)
Так как 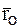 ,
,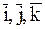 определяют положение подвижной системы координат, т. е. являются параметрами переносного движения МТ (производные от координат x, y, z не входят в это выражение, т. е. МТ как бы не перемещается относительно подвижной системы координат), то в выражении (7.2):
определяют положение подвижной системы координат, т. е. являются параметрами переносного движения МТ (производные от координат x, y, z не входят в это выражение, т. е. МТ как бы не перемещается относительно подвижной системы координат), то в выражении (7.2):
 . (7.5)
. (7.5)
Используя формулу (1.21), получим:
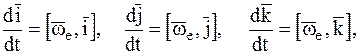 (7.6)
(7.6)
где  — переносная угловая скорость, т. е. угловая скорость вращения подвижной системы координат относительно неподвижной и тогда соотношение (7.5) примет вид:
— переносная угловая скорость, т. е. угловая скорость вращения подвижной системы координат относительно неподвижной и тогда соотношение (7.5) примет вид:
 . (7.7)
. (7.7)

Рис. 65
Подставив выражения (7.3) — (7.5) в выражение (7.2), получим теорему о сложении скоростей в сложном движении МТ:
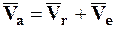 . (7.8)
. (7.8)
Теорема: Абсолютная скорость сложного движения МТ равна геометрической сумме переносной и относительной скоростей этой МТ (рис. 65).
 2014-02-02
2014-02-02 540
540








