Теорема о сложении ускорений МТ

Возьмем производную по времени от выражения (7.2):

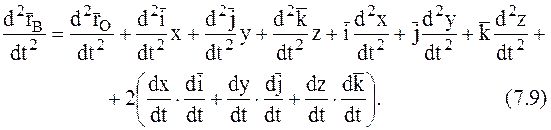
Здесь, если использовать те же пояснения, что и для формул (7.3) — (7.7), то:

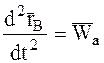, (7.10)

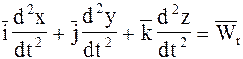, (7.11)

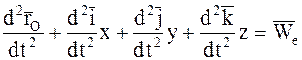, (7.12)

или 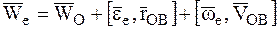. (7.13)

Еще одна последняя группа слагаемых в выражении (7.9) не может быть отнесена по смыслу ни к выражению (7.11), ни к (7.12), так как они содержат производную от всех переменных 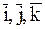, x, y, z. Обозначим эту группу слагаемых через :

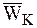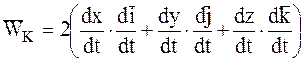. (7.14)

Подставив соотношения (7.6) в выражение (7.14), получим:

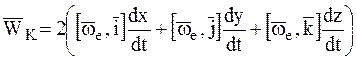или

.

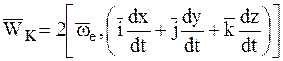Используя соотношение (7.4), выражение для 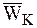можно записать в виде:

. (7.15)

Ускорение 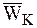называется ускорением Кориолиса или поворотным ускорением и является результатом взаимного влияния переносного и относительного движений.

Соотношение (7.9) с учетом выражений (7.10) — (7.14) принимает вид:

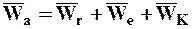. (7.16)

Теорема: Абсолютное ускорение сложного движения МТ равно геометрической сумме переносного и относительного ускорений и ускорения Кориолиса (рис. 66).

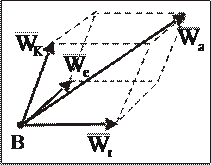
Рис. 66

Эту теорему называют также теоремой Кориолиса.