Ускорение Кориолиса

Из формул (7.15) следует, что ускорение Кориолиса равно удвоенному векторному произведению угловой скорости переносного движения на линейную скорость относительного движения.

На основании определения векторного произведения из формулы (7.15) можно получить модуль ускорения Кориолиса:

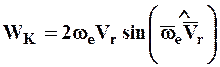. (7.17)

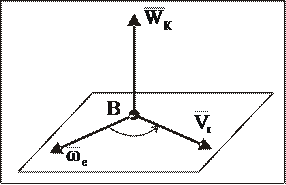
Рис. 67

Для определения направления ускорения Кориолиса нужно мысленно перенести параллельно самому себе вектор 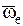в рассматриваемую МТ и использовать правило векторного произведения:

· ,

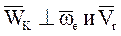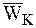· направлено в ту сторону, чтобы глядя с его конца, поворот от 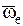к 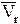был виден против хода часовой стрелки (рис. 67).

Найдем условия отсутствия ускорения Кориолиса (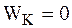) из формулы (7.17):

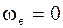· – угловая переносная скорость равна нулю в данный момент времени или переносное движение поступательное;

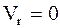· – относительная скорость равна нулю в данный момент времени (МТ не перемещается относительно подвижной системы координат в данный момент времени – относительный покой);

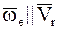· – относительное движение МТ в данный момент времени происходит по направлению, параллельному оси вращения переносного движения.

В этих трех случаях формула (7.16) имеет вид:

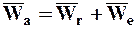, (7.18)

Т. е. абсолютное ускорение МТ в этих случаях равно геометрической сумме ускорений относительного и переносного движений.

Каким образом проявляет себя ускорение Кориолиса в случае переносного вращательного движения, будет продемонстрировано в примерах с использованием алгоритма К07 СДТ, особенно в примере 4, где рассматривается движение МТ по поверхности Земли с учетом переносного вращательного движения Земли.